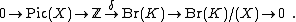请输入您要查询的百科知识：

　

词条 Severi–Brauer variety
释义

  1. See also

  2. Note

  3. References

  4. Further reading

  5. External links

In mathematics, a Severi–Brauer variety over a field K is an algebraic variety V which becomes isomorphic to a projective space over an algebraic closure of K. The varieties are associated to central simple algebras in such a way that the algebra splits over K if and only if the variety has a point rational over K.[1] {{harvs|txt|first=Francesco |last=Severi|authorlink=Francesco Severi|year=1932}} studied these varieties, and they are also named after Richard Brauer because of their close relation to the Brauer group.

In dimension one, the Severi–Brauer varieties are conics. The corresponding central simple algebras are the quaternion algebras. The algebra (a,b)K corresponds to the conic C(a,b) with equation

and the algebra (a,b)K splits, that is, (a,b)K is isomorphic to a matrix algebra over K, if and only if C(a,b) has a point defined over K: this is in turn equivalent to C(a,b) being isomorphic to the projective line over K.[1][2]

Such varieties are of interest not only in diophantine geometry, but also in Galois cohomology. They represent (at least if K is a perfect field) Galois cohomology classes in

H1(PGLn),

where PGLn

is the projective linear group, and n is the dimension of

the variety V. There is a short exact sequence

1 → GL1 → GLn → PGLn → 1

of algebraic groups. This implies a connecting homomorphism

H1(PGLn) → H2(GL1)

at the level of cohomology. Here H2(GL1) is identified with the Brauer group of K, while the kernel is trivial because

H1(GLn) = {1}

by an extension of Hilbert's Theorem 90.[3][4] Therefore, Severi–Brauer varieties can be faithfully represented by Brauer group elements, i.e. classes of central simple algebras.

Lichtenbaum showed that if X is a Severi–Brauer variety over K then there is an exact sequence

Here the map δ sends 1 to the Brauer class corresponding to X.[2]

As a consequence, we see that if the class of X has order d in the Brauer group then there is a divisor class of degree d on X. The associated linear system defines the d-dimensional embedding of X over a splitting field L.[5]

See also

  • projective bundle

Note

1. ^1 Jacobson (1996) p.113
2. ^1 Gille & Szamuely (2006) p.129
3. ^Gille & Szamuely (2006) p.26
4. ^{{citation | title=An Introduction to Galois Cohomology and its Applications | volume=377 | series=London Mathematical Society Lecture Note Series | first=Grégory | last=Berhuy | publisher=Cambridge University Press | year=2010 | isbn=0-521-73866-0 | zbl=1207.12003 | page=113 }}
5. ^Gille & Szamuely (2006) p.131

References

  • {{Citation | last1=Artin | first1=Michael | author1-link=Michael Artin | title=Brauer groups in ring theory and algebraic geometry (Wilrijk, 1981) | publisher=Springer-Verlag | location=Berlin, New York | others=Notes by A. Verschoren | series=Lecture Notes in Math. | isbn=978-3-540-11216-7 | doi=10.1007/BFb0092235 | mr=657430 | year=1982 | volume=917 | chapter=Brauer-Severi varieties | zbl=0536.14006 | pages=194–210}}
  • {{Springer|id=b/b017620|title=Brauer–Severi variety}}
  • {{citation | chapterurl=http://ebooks.cambridge.org/chapter.jsf?bid=CBO9780511607219&cid=CBO9780511607219A036 | pages=114–134 | title=Central Simple Algebras and Galois Cohomology | chapter=Severi–Brauer varieties | first1=Philippe | last1=Gille | first2=Tamás | last2=Szamuely | series=Cambridge Studies in Advanced Mathematics | volume=101 | publisher=Cambridge University Press | year=2006 | isbn=0-521-86103-9 | zbl=1137.12001 | mr=2266528}}
  • {{citation | last=Jacobson | first=Nathan | authorlink=Nathan Jacobson | title=Finite-dimensional division algebras over fields | zbl=0874.16002 | location=Berlin | publisher=Springer-Verlag | isbn=3-540-57029-2 | year=1996 }}
  • {{citation | last=Saltman | first=David J. | title=Lectures on division algebras | series=Regional Conference Series in Mathematics | volume=94 | location=Providence, RI | publisher=American Mathematical Society | year=1999 | isbn=0-8218-0979-2 | zbl=0934.16013 }}
  • {{Citation | last1=Severi | first1=Francesco | title=Un nuovo campo di ricerche nella geometria sopra una superficie e sopra una varietà algebrica | language=Italian | id=Reprinted in volume 3 of his collected works | year=1932 | journal=Memorie della Reale Accademia d'Italia | volume=3 | issue=5}}

Further reading

  • {{citation | last1=Knus | first1=Max-Albert | last2=Merkurjev | first2=Alexander | author2-link=Alexander Merkurjev | last3=Rost | first3=Markus | author3-link=Markus Rost | last4=Tignol | first4=Jean-Pierre | title=The book of involutions | others=With a preface by J. Tits | zbl=0955.16001 | series=Colloquium Publications | publisher=American Mathematical Society | volume=44 | location=Providence, RI | year=1998 | isbn=0-8218-0904-0 | mr=1632779}}

External links

  • Expository paper on Galois descent (PDF)
{{DEFAULTSORT:Severi-Brauer Variety}}

5 : Algebraic varieties|Diophantine geometry|Homological algebra|Algebraic groups|Ring theory
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/9/30 18:26:58