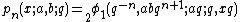“Little q-Jacobi polynomials”的意思、由来-开放百科全书

词条

Little q-Jacobi polynomials

释义

Definition
Orthogonality
Recurrence and difference relations
Rodrigues formula
Generating function
Relation to other polynomials
Gallery
References

In mathematics, the little q-Jacobi polynomials p_n(x;a,b;q) are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme, introduced by {{harvtxt|Hahn|1949}}. {{harvs|txt | last1=Koekoek | first1=Roelof | last2=Lesky | first2=Peter A. | last3=Swarttouw | first3=René F. | title=Hypergeometric orthogonal polynomials and their q-analogues | publisher=Springer-Verlag | location=Berlin, New York | series=Springer Monographs in Mathematics | isbn=978-3-642-05013-8 | doi=10.1007/978-3-642-05014-5 | mr=2656096 | year=2010|loc=14}} give a detailed list of their properties.

Definition

The little q-Jacobi polynomials are given in terms of basic hypergeometric functions and the Pochhammer symbol by

Orthogonality

Recurrence and difference relations

Rodrigues formula

Generating function

Relation to other polynomials

Gallery

The following are a set of animation plots for Little q-Jacobi polynomials, with varying q;

three density plots of imaginary, real and modula in complex space; three set of complex 3D plots

of imaginary, real and modulus of the said polynomials.

References

{{Citation | last1=Gasper | first1=George | last2=Rahman | first2=Mizan | title=Basic hypergeometric series | publisher=Cambridge University Press | edition=2nd | series=Encyclopedia of Mathematics and its Applications | isbn=978-0-521-83357-8 | doi=10.2277/0521833574 | mr=2128719 | year=2004 | volume=96}}
{{Citation | last1=Hahn | first1=Wolfgang | title=Über Orthogonalpolynome, die q-Differenzengleichungen genügen | doi=10.1002/mana.19490020103 | mr=0030647 | year=1949 | journal=Mathematische Nachrichten | issn=0025-584X | volume=2 | pages=4–34}}
{{Citation | last1=Koekoek | first1=Roelof | last2=Lesky | first2=Peter A. | last3=Swarttouw | first3=René F. | title=Hypergeometric orthogonal polynomials and their q-analogues | publisher=Springer-Verlag | location=Berlin, New York | series=Springer Monographs in Mathematics | isbn=978-3-642-05013-8 | doi=10.1007/978-3-642-05014-5 | mr=2656096 | year=2010}}
{{dlmf|id=18|first=Tom H. |last=Koornwinder|first2=Roderick S. C.|last2= Wong|first3=Roelof |last3=Koekoek||first4=René F. |last4=Swarttouw}}

3 : Orthogonal polynomials|Q-analogs|Special hypergeometric functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。