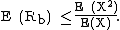- Statement of inequality Proof
- See also
- References
In probability theory, Lorden's inequality is a bound for the moments of overshoot for a stopped sum of random variables, first published by Gary Lorden in 1970.[1] Overshoots play a central role in renewal theory.[2]
Statement of inequality
Let X1, X2, ... be independent and identially distributed positive random variables and define the sum Sn = X1 + X2 + ... + Xn. Consider the first time Sn exceeds a given value b and at that time compute Rb = Sn − b. Rb is called the overshoot or excess at b. Lorden's inequality states that the expectation of this overshoot is bounded as[2]
Proof
Three proofs are known due to Lorden,[1] Carlsson and Nerman[3] and Chang.[4]
See also
- Wald's equation
References
1. ^1 {{Cite journal | last1 = Lorden | first1 = G. | title = On Excess over the Boundary | doi = 10.1214/aoms/1177697092 | journal = The Annals of Mathematical Statistics | volume = 41 | issue = 2 | pages = 520 | year = 1970 | pmid = | pmc = | jstor = 2239350}}
2. ^1 {{Cite journal | last1 = Spouge | first1 = John L. | title = Inequalities on the overshoot beyond a boundary for independent summands with differing distributions | doi = 10.1016/j.spl.2007.02.013 | journal = Statistics & Probability Letters | volume = 77 | issue = 14 | pages = 1486–1489 | year = 2007 | pmid = | pmc = 2683021}}
3. ^{{cite journal | last1 = Carlsson | first1 = Hasse | last2 = Nerman | first2 = Olle | year = 1986 | title = An Alternative Proof of Lorden's Renewal Inequality | journal = Advances in Applied Probability | volume = 18 | issue = 4 | pages = 1015–1016 | publisher = Applied Probability Trust |jstor=1427260}}
4. ^{{Cite journal | last1 = Chang | first1 = J. T. | title = Inequalities for the Overshoot | doi = 10.1214/aoap/1177004913 | journal = The Annals of Applied Probability | volume = 4 | issue = 4 | pages = 1223 | year = 1994 | pmid = | pmc = }}
{{probability-stub}}2. ^1 {{Cite journal | last1 = Spouge | first1 = John L. | title = Inequalities on the overshoot beyond a boundary for independent summands with differing distributions | doi = 10.1016/j.spl.2007.02.013 | journal = Statistics & Probability Letters | volume = 77 | issue = 14 | pages = 1486–1489 | year = 2007 | pmid = | pmc = 2683021}}
3. ^{{cite journal | last1 = Carlsson | first1 = Hasse | last2 = Nerman | first2 = Olle | year = 1986 | title = An Alternative Proof of Lorden's Renewal Inequality | journal = Advances in Applied Probability | volume = 18 | issue = 4 | pages = 1015–1016 | publisher = Applied Probability Trust |jstor=1427260}}
4. ^{{Cite journal | last1 = Chang | first1 = J. T. | title = Inequalities for the Overshoot | doi = 10.1214/aoap/1177004913 | journal = The Annals of Applied Probability | volume = 4 | issue = 4 | pages = 1223 | year = 1994 | pmid = | pmc = }}
2 : Stochastic processes|Probabilistic inequalities
- 18th Legislative Assembly of Saskatchewan
- 18th Logistics Battalion
- 18th Lorried Infantry Brigade (United Kingdom)
- 18th Lumières Awards
- 18th Maccabiah
- 18th Man
- 18th (Manitoba) Armoured Car Regiment
- 18th Manitoba Legislature
- 18th (Marmaduke's) Arkansas Infantry Regiment
- 18th (Marmaduke’s) Arkansas Infantry Regiment
- 18th Moscow Film Festival
- 18th Moscow International Film Festival
- 18th Mounted Brigade
- 18th Mounted Brigade (United Kingdom)
- 18th National Congress of Kuomintang
- 18th National Film Awards
- 18th National Television Awards
- 18th New Brunswick Legislative Assembly
- 18th New York State Legislature
- 18th New Zealand Parliament
- 18th November Torchlight procession
- 18th Oklahoma Legislature
- 18th Orgburo of the All-Union Communist Party (Bolsheviks)
- 18th Panzer Division (Germany)
- 18th Panzergrenadier Division (Wehrmacht)