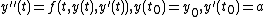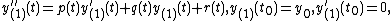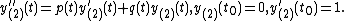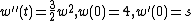1. Linear shooting method

2. Example

3. See also

4. Notes

5. References

6. External links

In numerical analysis, the shooting method is a method for solving a boundary value problem by reducing it to the solution of an initial value problem. Roughly speaking, we 'shoot' out trajectories in different directions until we find a trajectory that has the desired boundary value. The following exposition may be clarified by this illustration of the shooting method.

For a boundary value problem of a second-order ordinary differential equation, the method is stated as follows.

Let

be the boundary value problem.

Let y(t; a) denote the solution of the initial value problem

Define the function F(a) as the difference between y(t₁; a) and the specified boundary value y₁.

If F has a root a then the solution y(t; a) of the corresponding initial value problem is also a solution of the boundary value problem.

Conversely, if the boundary value problem has a solution y(t), then y(t) is also the unique solution y(t; a) of the initial value problem where a = y'(t₀), thus a is a root of F.

The usual methods for finding roots may be employed here,

such as the bisection method or Newton's method.

Linear shooting method

The boundary value problem is linear if f has the form

In this case, the solution to the boundary value problem is usually given by:

where 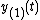is the solution to the initial value problem:

and is the solution to the initial value problem:

See [https://web.archive.org/web/20061209234620/http://math.fullerton.edu/mathews/n2003/shootingmethod/ShootingProof.pdf the proof] for the precise condition under which this result holds.

Example

A boundary value problem is given as follows by Stoer and Burlisch^[1] (Section 7.3.1).

The initial value problem

was solved for s = −1, −2, −3, ..., −100, and F(s) = w(1;s) − 1 plotted in the first figure.

Inspecting the plot of F,

we see that there are roots near −8 and −36.

Some trajectories of w(t;s) are shown in the second figure.

Stoer and Burlisch^[1] state that there are two solutions,

which can be found by algebraic methods.

These correspond to the initial conditions w′(0) = −8 and w′(0) = −35.9 (approximately).

See also

• Direct multiple shooting method
• Computation of radiowave attenuation in the atmosphere

Notes

References

• {{Cite book | last1=Press | first1=WH | last2=Teukolsky | first2=SA | last3=Vetterling | first3=WT | last4=Flannery | first4=BP | year=2007 | title=Numerical Recipes: The Art of Scientific Computing | edition=3rd | publisher=Cambridge University Press | publication-place=New York | isbn=978-0-521-88068-8 | chapter=Section 18.1. The Shooting Method | chapter-url=http://apps.nrbook.com/empanel/index.html#pg=959}}

External links

• Brief Description of ODEPACK (at Netlib; contains LSODE)
• Shooting method of solving boundary value problems – Notes, PPT, Maple, Mathcad, Matlab, Mathematica at Holistic Numerical Methods Institute  

• Shelley, ID
• Shelley, Idaho
• Shelley Jackson
• Shelley Lee Long
• Shelley Long
• Shelley Martel
• Shelley Moore Capito
• Shelley Morrison
• Shelley Peterson
• Shelley Smith (sports reporter)
• Shelley's rule
• Shelley Unwin
• Shelley versus Kraemer
• Shelley v. Kramer
• Shelley Wark-Martyn
• Shelley, Western Australia
• Shelley, West Yorkshire
• Shelley Winters
• Shellfish
• Shell fragments
• Shell game
• Shell Game (short story)
• Shell Game (Short Story)
• Shell Gas & Power
• Shell ginger