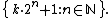1. Known Sierpiński numbers

2. Sierpiński problem

3. Prime Sierpiński problem

4. Extended Sierpiński problem

5. Simultaneously Sierpiński and Riesel

6. Dual Sierpinski problem

7. See also

8. References

9. Further reading

10. External links

In number theory, a Sierpinski or Sierpiński number is an odd natural number k such that is composite, for all natural numbers n. In 1960, Wacław Sierpiński proved that there are infinitely many odd integers k which have this property.

In other words, when k is a Sierpiński number, all members of the following set are composite:

Numbers in such a set with odd k and {{nowrap|k < 2ⁿ}} are Proth numbers.

Known Sierpiński numbers

The sequence of currently known Sierpiński numbers begins with:

78557, 271129, 271577, 322523, 327739, 482719, 575041, 603713, 903983, 934909, 965431, 1259779, 1290677, 1518781, 1624097, 1639459, 1777613, 2131043, 2131099, 2191531, 2510177, 2541601, 2576089, 2931767, 2931991, ... {{OEIS|id=A076336}}.

The number 78557 was proved to be a Sierpiński number by John Selfridge in 1962, who showed that all numbers of the form {{nowrap|78557⋅2ⁿ + 1}} have a factor in the covering set {{math|{3, 5, 7, 13, 19, 37, 73}}}. For another known Sierpiński number, 271129, the covering set is {{math|{3, 5, 7, 13, 17, 241}}}. Most currently known Sierpiński numbers possess similar covering sets.^[1]

However, in 1995 A. S. Izotov showed that some fourth powers could be proved to be Sierpiński numbers without establishing a covering set for all values of n. His proof depends on the aurifeuillean factorization {{math|1=t⁴⋅2⁴ⁿ⁺² + 1 = (t²⋅2²ⁿ⁺¹ + t⋅2ⁿ⁺¹ + 1)⋅(t²⋅2²ⁿ⁺¹ - t⋅2ⁿ⁺¹ + 1)}}. This establishes that all {{math|n ≡ 2 (mod 4)}} give rise to a composite, and so it remains to eliminate only {{math|n ≡ 0, 1, 3 (mod 4)}} using a covering set.^[2] Take {{math|1=t⁴ = 44745755⁴}} for an explicit example.^[3]

Sierpiński problem

The Sierpiński problem is: "What is the smallest Sierpiński number?"

In 1967, Sierpiński and Selfridge conjectured that 78,557 is the smallest Sierpiński number, and thus the answer to the Sierpiński problem.

To show that 78,557 really is the smallest Sierpiński number, one must show that all the odd numbers smaller than 78,557 are not Sierpiński numbers. That is, for every odd k below 78,557 there exists a positive integer n such that k2ⁿ+1 is prime.^[1] {{As of|2018|11}}, there are only five candidates:

k = 21181, 22699, 24737, 55459, and 67607

which have not been eliminated as possible Sierpiński numbers.^[4]

Prime Sierpiński problem

In 1976, Nathan Mendelsohn determined that the second provable Sierpiński number is the prime k = 271129. The prime Sierpiński problem asks "what is the smallest prime Sierpiński number", and there is an ongoing "Prime Sierpiński search" which tries to prove that 271129 is the first Sierpiński number which is also a prime. The prime values of k less than 271129 for which a prime of the form k2ⁿ+1 is not known {{As of|2018|11}} are:

k = 22699, 67607, 79309, 79817, 152267, 156511, 222113, 225931, 237019.

The first two, being less than 78557, are also unsolved cases of the (non-prime) Sierpiński problem described above.

Extended Sierpiński problem

Suppose that both preceding Sierpiński problems had finally been solved, showing that 78557 is the smallest Sierpiński number and that 271129 is the smallest prime Sierpiński number. This still leaves unsolved the question of the second Sierpinski number; there could exist a composite Sierpiński number k such that . A ongoing search is trying to prove that 271129 is the second Sierpiński number, by testing all k values between 78557 and 271129, prime or not.

Solving the extended Sierpiński problem, the most demanding of the three posed problems, requires the elimination of 23 remaining candidates , of which nine are prime (see above) and fourteen are composite. The latter include k = 21181, 24737, 55459 from the original Sierpiński problem, unique to the extended Sierpiński problem. {{as of|2018|04}}, the following ten values of k remain:

k = 91549, 99739, 131179, 163187, 200749, 202705, 209611, 227723, 229673, 238411.

The distributed volunteer computing project PrimeGrid is attempting to eliminate all the remaining values of k. {{as of|2018|04}}, no prime has been found for these values of k with 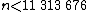.^[5]

The most recent elimination was in April 2018, when was found to be prime by PrimeGrid, eliminating k=193997. The number is 3,447,670 digits long.^[6]

Simultaneously Sierpiński and Riesel

A number may be simultaneously Sierpiński and Riesel. These are called Brier numbers. The smallest five known examples are 3316923598096294713661, 10439679896374780276373, 11615103277955704975673, 12607110588854501953787, 17855036657007596110949, ... ({{OEIS link|A076335}}).^[7]

Dual Sierpinski problem

If we take the n of k2ⁿ + 1 to be a negative integer, then the number become 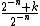. If we choose the numerator, then the number become 2⁻ⁿ + k. Thus, a dual Sierpinski number is defined as an odd natural number k such that {{nowrap|2ⁿ + k}} is composite for all natural numbers n. There is a conjecture that the set of these numbers is the same as the set of Sierpinski numbers; for example, {{nowrap|2ⁿ + 78557}} is composite for all natural numbers n.

The least n such that {{nowrap|2ⁿ + k}} is prime are (for odd ks)

1, 1, 1, 2, 1, 1, 2, 1, 1, 2, 1, 3, 2, 1, 1, 4, 2, 1, 2, 1, 1, 2, 1, 5, 2, 1, 3, 2, 1, 1, 8, 2, 1, 2, 1, 1, 4, 2, 1, 2, 1, 7, 2, 1, 3, 4, 2, 1, 2, 1, 1, 2, 1, 1, 2, 1, 7, 4, 5, 3, 4, 2, 1, 2, 1, 3, 2, 1, 1, 10, 3, 3, 2, 1, 1, ... {{OEIS|id=A067760}}

The odd ks which {{nowrap|2ⁿ + k}} are composite for all {{nowrap|n < k}} are

773, 2131, 2491, 4471, 5101, 7013, 8543, 10711, 14717, 17659, 19081, 19249, 20273, 21661, 22193, 26213, 28433, ... {{OEIS|id=A033919}}

There is also a "five or bust", similar to seventeen or bust, considers this problem, and found (probable) primes for all {{nowrap|k < 78557}} (the largest prime is 2^9092392 + 40291^[8]), so it is currently known that 78557 is the smallest dual Sierpinski number.

See also

• Cullen number
• Proth number
• Riesel number
• Seventeen or Bust

References

Further reading

• {{citation |first=Richard K. |last=Guy |authorlink=Richard K. Guy |title=Unsolved Problems in Number Theory |publisher=Springer-Verlag |location=New York |year=2004 |page=120 |isbn=0-387-20860-7 }}

External links

• The Sierpinski problem: definition and status
• {{MathWorld| urlname=SierpinskisCompositeNumberTheorem |title=Sierpinski's composite number theorem}}
• {{cite web|last1=Grime|first1=Dr. James|title=78557 and Proth Primes|url=https://www.youtube.com/watch?v=fcVjitaM3LY|website=YouTube|publisher=Brady Haran|accessdate=13 November 2017|format=video}}

• Humeston (IA)
• Hume's treecreeper
• Hume's wheatear
• Hume Township, Whiteside County, Illinois
• Humeur
• Hume, VA
• Hume, Virginia
• Humewood-Cedervale
• Humewood–Cedarvale
• Hum (film)
• Humfrey
• Humfrey of Lancaster
• Humfrey Payne
• Humfrid
• Humfrid (bishop)
• Humfrid, Count of Barcelona
• Humfridus
• Humfry Payne
• Hum halalujah
• Hum Hallelujah
• Hum Hindustani
• Humiaki Huzita
• Humic
• Humic matter
• Humic substances