“Simplicial manifold”的意思、由来-开放百科全书

词条

Simplicial manifold

释义

A manifold made out of simplices
A simplicial object built from manifolds

In physics, the term simplicial manifold commonly refers to one of several loosely defined objects, commonly appearing in the study of Regge calculus. These objects combine attributes of a simplex with those of a manifold. There is no standard usage of this term in mathematics, and so the concept can refer to a triangulation in topology, or a piecewise linear manifold, or one of several different functors from either the category of sets or the category of simplicial sets to the category of manifolds.

A manifold made out of simplices

A simplicial manifold is a simplicial complex for which the geometric realization is homeomorphic to a topological manifold. This is essentially the concept of a triangulation in topology. This can mean simply that a neighborhood of each vertex (i.e. the set of simplices that contain that point as a vertex) is homeomorphic to a n-dimensional ball.

A simplicial object built from manifolds

A simplicial manifold is also a simplicial object in the category of manifolds. This is a special case of a simplicial space in which, for each n, the space of n-simplices is a manifold.

For example, if G is a Lie group, then the simplicial nerve of G has the manifold 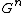as its space of n-simplices. More generally, G can be a Lie groupoid.

2 : Structures on manifolds|Simplicial sets

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。