- Definition
- Properties of the medcouple The medcouple kernel Robustness Values
- Algorithms for computing the medcouple Naïve algorithm Fast algorithm Comparing a value against the kernel matrix Weighted median of row medians Kth pair algorithm
- Software/source code
- See also
- References
In statistics, the medcouple is a robust statistic that measures the skewness of a univariate distribution. It is defined as a scaled median difference of the left and right half of a distribution. Its robustness makes it suitable for identifying outliers in adjusted boxplots.[2][3] Ordinary box plots do not fare well with skew distributions, since they label the longer unsymmetrical tails as outliers. Using the medcouple, the whiskers of a boxplot can be adjusted for skew distributions and thus have a more accurate identification of outliers for non-symmetrical distributions.
As a kind of order statistic, the medcouple belongs to the class of incomplete generalised L-statistics. Like the ordinary median or mean, the medcouple is a nonparametric statistic, thus it can be computed for any distribution.
Definition
In order to harmonise with zero-based indexing in many programming languages, we will index from zero in all that follows.
Let 
be an ordered sample of size 
, and let 
be the median of 
. Define the sets
,
,
of sizes 
and 
respectively. For 
and 
, we define the kernel function
where 
is the sign function.
The medcouple is then the median of the set{{rp|998}}
.
In other words, we split the distribution into all values greater or equal to the median and all values less than or equal to the median. We define a kernel function whose first variable is over the 
greater values and whose second variable is over the 
lesser values. For the special case of values tied to the median, we define the kernel by the signum function. The medcouple is then the median over all 
values of 
.
Since the medcouple is not a median applied to all 
couples, but only to those for which 
, it belongs to the class of incomplete generalised L-statistics.{{rp|998}}
Properties of the medcouple
The medcouple has a number of desirable properties. A few of them are directly inherited from the kernel function.
The medcouple kernel
We make the following observations about the kernel function :
- The kernel function is location-invariant.{{rp|999}} If we add or subtract any value to each element of the sample , the corresponding values of the kernel function do not change.
- The kernel function is scale-invariant.{{rp|999}} Equally scaling all elements of the sample does not alter the values of the kernel function.
These properties are in turn inherited by the medcouple. Thus, the medcouple is independent of the mean and standard deviation of a distribution, a desirable property for measuring skewness.
For ease of computation, these properties enable us to define the two sets
where 
. This makes the set 
have range of at most 1, median 0, and keep the same medcouple as .
For 
, the medcouple kernel reduces to
Using the recentred and rescaled set we can observe the following.
- The kernel function is between -1 and 1,{{rp|998}} that is,
. This follows from the reverse triangle inequality 
with 
and 
and the fact that 
. - The medcouple kernel
is non-decreasing in each variable.{{rp|1005}} This can be verified by the partial derivatives 
and 
, both nonnegative, since .
With properties 1, 2, and 4, we can thus define the following matrix,
If we sort the sets 
and 
in decreasing order, then the matrix 
has sorted rows and sorted columns,{{rp|1006}}
The medcouple is then the median of this matrix with sorted rows and sorted columns. The fact that the rows and columns are sorted allows the implementation of a fast algorithm for computing the medcouple.
Robustness
The breakdown point is the number of values that a statistic can resist before it becomes meaningless, i.e. the number of arbitrarily large outliers that the data set may have before the value of the statistic is affected. For the medcouple, the breakdown point is 25%, since it is a median taken over the couples such that 
.{{rp|1002}}
Values
Like all measures of skewness, the medcouple is positive for distributions that are skewed to the right, negative for distributions skewed to the left, and zero for symmetrical distributions. In addition, the values of the medcouple are bounded by 1 in absolute value.{{rp|998}}
Algorithms for computing the medcouple
Before presenting medcouple algorithms, we recall that there exist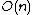 
algorithms for the finding the median. Since the medcouple is a median, ordinary algorithms for median-finding are important.
Naïve algorithm
The naïve algorithm for computing the medcouple is slow.{{rp|1005}} It proceeds in two steps. First, it constructs the medcouple matrix which contains all of the possible values of the medcouple kernel. In the second step, it finds the median of this matrix. Since there are 
entries in the matrix in the case when all elements of the data set are unique, the algorithmic complexity of the naïve algorithm is 
.
More concretely, the naïve algorithm proceeds as follows. Recall that we are using zero-based indexing.
'''function''' naïve_medcouple('''vector''' X): ''// X is a vector of size n.'' ''//Sorting in decreasing order can be done in-place in O(n log n) time''sort_decreasing(X)
xm := median(X) xscale := 2*max(X) ''// define the upper and lower centred and rescaled vectors'' ''// they inherit X's own decreasing sorting Zplus := [(x - xm)/xscale | x '''in''' X '''such that''' x >= xm] Zminus := [(x - xm)/xscale | x '''in''' X '''such that''' x <= xm] p := size(Zplus) q := size(Zminus) ''// define the kernel function closing over Zplus and Zminus'' '''function''' h(i,j): a := Zplus[i] b := Zminus[j] '''if''' a == b: '''return''' signum(p - 1 - i - j) '''else''': '''return''' (a + b)/(a - b) '''endif''' '''endfunction''' ''// O(n^2) operations necessary to form this vector'' H := [h(i,j) | i '''in''' [0, 1, ..., p - 1] '''and''' j '''in''' [0, 1, ..., q - 1]] '''return''' median(H) '''endfunction'''
The final call to median on a vector of size can be done itself in operations, hence the entire naïve medcouple algorithm is of the same complexity.
Fast algorithm
The fast algorithm outperforms the naïve algorithm by exploiting the sorted nature of the medcouple matrix . Instead of computing all entries of the matrix, the fast algorithm uses the Kth pair algorithm of Johnson & Mizoguchi.[15]
The first stage of the fast algorithm proceeds as the naïve algorithm. We first compute the necessary ingredients for the kernel matrix, 
, with sorted rows and sorted columns in decreasing order. Rather than computing all values of 
, we instead exploit the monotonicity in rows and columns, via the following observations.
Comparing a value against the kernel matrix
First, we note that we can compare any 
with all values of in 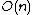time.[15]{{rp|150}} For example, for determining all 
and 
such that 
, we have the following function:
'''function''' greater_h('''kernel''' h, '''int''' p, '''int''' q, '''real''' u): ''// h is the kernel function, h(i,j) gives the ith, jth entry of H'' ''// p and q are the number of rows and columns of the kernel matrix H'' ''// vector of size p'' P := '''vector'''(p) ''// indexing from zero'' j := 0 ''// starting from the bottom, compute the least upper bound for each row'' '''for''' i := p - 1, p - 2, ..., 1, 0: ''// search this row until we find a value less than u'' '''while''' j < q '''and''' h(i, j) > u: j := j + 1 '''endwhile''' ''// the entry preceding the one we just found is greater than u P[i] := j - 1 '''endfor''' '''return''' P '''endfunction'''This greater_h function is traversing the kernel matrix from the bottom left to the top right, and returns a vector 
of indices that indicate for each row where the boundary lies between values greater than and those less than or equal to . This method works because of the row-column sorted property of . Since greater_h computes at most 
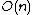values of , its complexity is .[15]{{rp|150}}
Conceptually, the resulting vector can be visualised as establishing a boundary on the matrix as suggested by the following diagram, where the red entries are all larger than :
The symmetric algorithm for computing the values of less than is very similar. It instead proceeds along in the opposite direction, from the top right to the bottom left:
'''function''' less_h('''kernel''' h, '''int''' p, '''int''' q, '''real''' u): ''// vector of size p'' Q := '''vector'''(p) ''// last possible row index'' j := q - 1 ''// starting from the top, compute the greatest lower bound for each row'' '''for''' i := 0, 1, ..., p - 2, p - 1: ''// search this row until we find a value greater than u'' '''while''' j >= 0 '''and''' h(i, j) < u: j := j - 1 '''endwhile''' ''// the entry following the one we just found is less than u Q[i] := j + 1 '''endfor''' '''return''' Q '''endfunction'''This lower boundary can be visualised like so, where the blue entries are smaller than :
For each , we have that 
, with strict inequality occurring only for those rows that have values equal to .
We also have that the sums
give, respectively, the number of elements of that are greater than , and the number of elements that are greater than or equal to . Thus this method also yields the rank of within the elements of .[15]{{rp|149}}
Weighted median of row medians
The second observation is that we can use the sorted matrix structure to instantly compare any element to at least half of the entries in the matrix. For example, the median of the row medians across the entire matrix is less than the upper left quadrant in red, but greater than the lower right quadrant in blue:
More generally, using the boundaries given by the and 
vectors from the previous section, we can assume that after some iterations, we have pinpointed the position of the medcouple to lie between the red left boundary and the blue right boundary:[15]{{rp|149}}
The yellow entries indicate the median of each row. If we mentally re-arrange the rows so that the medians align and ignore the discarded entries outside the boundaries,
we can select a weighted median of these medians, each entry weighted by the number of remaining entries on this row. This ensures that we can discard at least 1/4 of all remaining values no matter if we have to discard the larger values in red or the smaller values in blue:
Each row median can be computed in 
time, since the rows are sorted, and the weighted median can be computed in 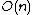time, using a binary search.[15]{{rp|148}}
Kth pair algorithm
Putting together these two observations, the fast medcouple algorithm proceeds broadly as follows.[15]{{rp|148}}
- Compute the necessary ingredients for the medcouple kernel function
with sorted rows and sorted columns. - At each iteration, approximate the medcouple with the weighted median of the row medians.&91;15&93;{{rp|148}}
- Compare this tentative guess to the entire matrix obtaining right and left boundary vectors and respectively. The sum of these vectors also gives us the rank of this tentative medcouple.
- If the rank of the tentative medcouple is exactly
, then stop. We have found the medcouple. - Otherwise, discard the entries greater than or less than the tentative guess by picking either or as the new right or left boundary, depending on which side the element of rank is in. This step always discards at least 1/4 of all remaining entries.
- If the rank of the tentative medcouple is exactly
- Once the number of candidate medcouples between the right and left boundaries is less than or equal to , perform a rank selection amongst the remaining entries, such that the rank within this smaller candidate set corresponds to the rank of the medcouple within the whole matrix.
The initial sorting in order to form the function takes 
time. At each iteration, the weighted median takes 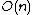time, as well as the computations of the new tentative and left and right boundaries. Since each iteration discards at least 1/4 of all remaining entries, there will be at most 
iterations.[15]{{rp|150}} Thus, the whole fast algorithm takes time.[15]{{rp|150}}
Let us restate the fast algorithm in more detail.
'''function''' medcouple('''vector''' X): ''// X is a vector of size n'' ''// compute initial ingredients as for the naïve medcouple''sort_decreasing(X)
xm := median(X) xscale := 2*max(X) Zplus := [(x - xm)/xscale | x '''in''' X '''such that''' x >= xm] Zminus := [(x - xm)/xscale | x '''in''' X '''such that''' x <= xm] p := size(Zplus) q := size(Zminus) '''function''' h(i,j): a := Zplus[i] b := Zminus[j] '''if''' a == b: '''return''' signum(p - 1 - i - j) '''else''': '''return''' (a + b)/(a - b) '''endif''' '''endfunction''' ''// begin Kth pair algorithm (Johnson & Mizoguchi)'' ''// the initial left and right boundaries, two vectors of size p'' L := [0, 0, ..., 0] R := [q - 1, q - 1, ..., q - 1] ''// number of entries to the left of the left boundary'' Ltotal := 0 ''// number of entries to the left of the right boundary'' Rtotal := p*q ''// since we are indexing from zero, the medcouple index is one'' ''// less than its rank'' medcouple_index := floor(Rtotal/2) ''// iterate while the number of entries between the boundaries is'' ''// greater than the number of rows in the matrix'' '''while''' Rtotal - Ltotal > p: ''// compute row medians and their associated weights, but skip'' ''// any rows that are already empty'' middle_idx := [i | i '''in''' [0, 1, ..., p - 1] '''such''' '''that''' L[i] <= R[i]] row_medians := [h(i, floor((L[i] + R[i])/2) | i '''in''' middle_idx] weights := [R[i] - L[i] + 1 | i '''in''' middle_idx] WM := weighted median(row_medians, weights) ''// new tentative right and left boundaries'' P := greater_h(h, p, q, WM) Q := less_h(h, p, q, WM) Ptotal := sum(P) + size(P) Qtotal := sum(Q) ''// determine which entries to discard, or if we've found the medcouple'' '''if''' medcouple_index <= Ptotal - 1: R := P Rtotal := Ptotal '''else''': '''if''' medcouple_index > Qtotal - 1: L := Q Ltotal := Qtotal '''else''': // found the medcouple, rank of the weighted median equals medcouple index '''return''' WM '''endif''' '''endif''' '''endwhile''' // did not find the medcouple, but there are very few tentative entries remaining remaining := [h(i,j) | i '''in''' [0, 1, ..., p - 1], j '''in''' [L[i], L[i] + 1, ..., R[i]] '''such''' '''that''' L[i] <= R[i] ] ''// select the medcouple by rank amongst the remaining entries'' medcouple := select_nth(remaining, medcouple_index - Ltotal) '''return''' medcouple '''endfunction'''
In real-world use, the algorithm also needs to account for errors arising from finite-precision floating point arithmetic. For example, the comparisons for the medcouple kernel function should be done within machine epsilon, as well as the order comparisons in the greater_h and less_h functions.
Software/source code
- The fast medcouple algorithm is implemented in R's robustbase package.
- A GPL'ed C++ implementation of the fast algorithm, derived from the R implementation.
- A Stata implementation of the fast algorithm.
- An implementation of the naïve algorithm in Matlab (and hence GNU Octave).
- The naïve algorithm is also implemented for the Python package statsmodels.
See also
{{Portal|Statistics}}- Robust statistic
- Skewness
- Adjusted boxplots
References
2. ^1 {{cite journal|author=M. Hubert|author2=E. Vandervieren|date=2008|title=An adjusted boxplot for skewed distributions|journal=Computational Statistics and Data Analysis|volume=52|issue=12|pages=5186–5201|doi=10.1016/j.csda.2007.11.008}}
3. ^1 2 3 4 5 6 7 8 9 10 {{cite journal|author=Donald B. Johnson|author2=Tetsuo Mizoguchi|date=May 1978|title=Selecting The Kth Element In X + Y And X1 + X2 +...+ Xm|journal=SIAM Journal on Computing|volume=7|issue=2|pages=147–153|doi=10.1137/0207013}}
}}
- Eleutherodactylus tinker
- Eleutherodactylus toftae
- Eleutherodactylus trachyblepharis
- Eleutherodactylus trepidotus
- Eleutherodactylus truebae
- Eleutherodactylus tubernasus
- Eleutherodactylus turpinorum
- Eleutherodactylus uisae
- Eleutherodactylus uranobates
- Eleutherodactylus variabilis
- Eleutherodactylus veletis
- Eleutherodactylus venancioi
- Eleutherodactylus ventrimarmoratus
- Eleutherodactylus verecundus
- Eleutherodactylus versicolor
- Eleutherodactylus vertebralis
- Eleutherodactylus vicarius
- Eleutherodactylus vidua
- Eleutherodactylus viejas
- Eleutherodactylus vinhai
- Eleutherodactylus viridicans
- Eleutherodactylus viridis
- Eleutherodactylus vocator
- Eleutherodactylus vulcani
- Eleutherodactylus walkeri