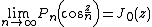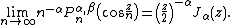“Mehler–Heine formula”的意思、由来-开放百科全书

词条

Mehler–Heine formula

释义

Legendre polynomials
Jacobi polynomials
References

In mathematics, the Mehler–Heine formula introduced by {{harvs|txt|authorlink=G. F. Mehler|last=Mehler|year=1868}} and {{harvs|txt|authorlink=Eduard Heine|last=Heine|year=1861}} describes the asymptotic behavior of the Legendre polynomials as the index tends to infinity, near the edges of the support of the weight. There are generalizations to other classical orthogonal polynomials, which are also called the Mehler–Heine formula. The formula complements the Darboux formulae which describe the asymptotics in the interior and outside the support.

Legendre polynomials

The simplest case of the Mehler–Heine formula states that

where P_n is the Legendre polynomial of order n, and J₀ a Bessel function. The limit is uniform over z in an arbitrary bounded domain in the complex plane.

Jacobi polynomials

The generalization to Jacobi polynomials P{{su|b=n|p=α,β}} is given by {{harv|Szegő|1939|loc=8.1}} as follows:

References

{{Citation | last1=Heine | first1=E. | title=Handbuch der Kugelfunktionen. Theorie und Anwendung. Neudruck. | url=https://books.google.com/books?id=D79hEMl2GM0C | publisher=Georg Reimer, Berlin | language=German | zbl=0103.29304 | year=1861 }}
{{Citation | last1=Mehler | first1=F. G. | title=Ueber die Vertheilung der statischen Elektricität in einem von zwei Kugelkalotten begrenzten Körper. | language=German | doi=10.1515/crll.1868.68.134 | year=1868 | journal=Journal für die Reine und Angewandte Mathematik | issn=0075-4102 | volume=68 | pages=134–150}}
{{Citation | last1=Szegő | first1=Gábor | title=Orthogonal Polynomials | url=https://books.google.com/books?id=3hcW8HBh7gsC | publisher= American Mathematical Society | series=Colloquium Publications | isbn=978-0-8218-1023-1 | mr=0372517 | year=1939 | volume=XXIII}}

1 : Orthogonal polynomials

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。