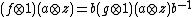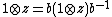- Statement
- Proof
- Notes
- References
In ring theory, a branch of mathematics, the Skolem–Noether theorem characterizes the automorphisms of simple rings. It is a fundamental result in the theory of central simple algebras.
The theorem was first published by Thoralf Skolem in 1927 in his paper Zur Theorie der assoziativen Zahlensysteme (German: On the theory of associative number systems) and later rediscovered by Emmy Noether.
Statement
In a general formulation, let A and B be simple unitary rings, and let k be the centre of B. Notice that k is a field since given x nonzero in k, the simplicity of B implies that the nonzero two-sided ideal BxB = (x) is the whole of B, and hence that x is a unit. If the dimension of B over k is finite, i.e. if B is a central simple algebra of finite dimension, and A is also a k-algebra, then given k-algebra homomorphisms
f, g : A → B,
there exists a unit b in B such that for all a in A[1][2]
g(a) = b · f(a) · b−1.
In particular, every automorphism of a central simple k-algebra is an inner automorphism.[3][4]
Proof
First suppose 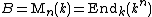 . Then f and g define the actions of A on
. Then f and g define the actions of A on  ; let
; let 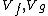 denote the A-modules thus obtained. Any two simple A-modules are isomorphic and
denote the A-modules thus obtained. Any two simple A-modules are isomorphic and 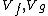 are finite direct sums of simple A-modules. Since they have the same dimension, it follows that there is an isomorphism of A-modules
are finite direct sums of simple A-modules. Since they have the same dimension, it follows that there is an isomorphism of A-modules 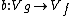 . But such b must be an element of
. But such b must be an element of 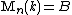 . For the general case, note that
. For the general case, note that 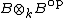 is a matrix algebra and that
is a matrix algebra and that 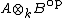 is simple. By the first part applied to the maps
is simple. By the first part applied to the maps 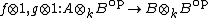 , there exists
, there exists 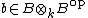 such that
such that
for all  and
and 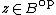 . Taking
. Taking  , we find
, we find
for all z. That is to say, b is in 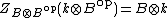 and so we can write
and so we can write 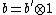 . Taking
. Taking 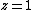 this time we find
this time we find
,
which is what was sought.
Notes
2. ^{{cite book|last=Farb|first=Benson|title=Noncommutative Algebra|year=1993|publisher=Springer|isbn=9780387940571|author2=Dennis, R. Keith }}
3. ^Gille & Szamuely (2006) p.40
4. ^Lorenz (2008) p.174
References
- {{cite journal | jfm=54.0154.02| journal=Skrifter Oslo | year=1927 | number=12 | pages=50 | language=German | first=Thoralf | last= Skolem | authorlink=Thoralf Skolem | title=Zur Theorie der assoziativen Zahlensysteme }}
- A discussion in Chapter IV of Milne, class field theory
- {{cite book | last1=Gille | first1=Philippe | last2=Szamuely | first2=Tamás | title=Central simple algebras and Galois cohomology | series=Cambridge Studies in Advanced Mathematics | volume=101 | location=Cambridge | publisher=Cambridge University Press | year=2006 | isbn=0-521-86103-9 | zbl=1137.12001 }}
- {{cite book | first=Falko | last=Lorenz | title=Algebra. Volume II: Fields with Structure, Algebras and Advanced Topics | year=2008 | publisher=Springer | isbn=978-0-387-72487-4 | zbl=1130.12001 }}
- San Francisco Chindua
- San Francisco Chontla Huasteco language
- San Francisco Choral Society
- San Francisco Chronicle Magazine
- San Francisco chronology
- San Francisco church
- San Francisco Church (Intramuros)
- San Francisco Church (La Paz)
- San Francisco Church of Intramuros
- San Francisco Church (Valparaiso)
- San Francisco Church, Valparaíso
- San Francisco City FC
- San Francisco City Guides
- San Francisco City League
- San Francisco Common Council
- San Francisco Community College District
- San Francisco Conservatory of Flowers
- San Francisco Costanoan
- San Francisco Costanoan language
- San Francisco Council
- San Francisco (county)
- San Francisco county
- San Francisco County Sheriff's Department
- San Francisco Damianas
- San Francisco de Asís