“Smith–Volterra–Cantor set”的意思、由来-开放百科全书

词条

Smith–Volterra–Cantor set

释义

Construction
Properties
Other fat Cantor sets
See also
References
External links

In mathematics, the Smith–Volterra–Cantor set (SVC), fat Cantor set, or ε-Cantor set^[1] is an example of a set of points on the real line ℝ that is nowhere dense (in particular it contains no intervals), yet has positive measure. The Smith–Volterra–Cantor set is named after the mathematicians Henry Smith, Vito Volterra and Georg Cantor. The Smith-Volterra-Cantor set is topologically equivalent to the middle-thirds Cantor set.

Construction

Similar to the construction of the Cantor set, the Smith–Volterra–Cantor set is constructed by removing certain intervals from the unit interval [0, 1].

The process begins by removing the middle 1/4 from the interval [0, 1] (the same as removing 1/8 on either side of the middle point at 1/2) so the remaining set is

The following steps consist of removing subintervals of width 1/4ⁿ from the middle of each of the 2ⁿ⁻¹ remaining intervals. So for the second step the intervals (5/32, 7/32) and (25/32, 27/32) are removed, leaving

Continuing indefinitely with this removal, the Smith–Volterra–Cantor set is then the set of points that are never removed. The image below shows the initial set and five iterations of this process.

Each subsequent iterate in the Smith–Volterra–Cantor set's construction removes proportionally less from the remaining intervals. This stands in contrast to the Cantor set, where the proportion removed from each interval remains constant. Thus, the former has positive measure while the latter has zero measure.

Properties

By construction, the Smith–Volterra–Cantor set contains no intervals and therefore has empty interior. It is also the intersection of a sequence of closed sets, which means that it is closed.

During the process, intervals of total length

are removed from [0, 1], showing that the set of the remaining points has a positive measure of 1/2. This makes the Smith–Volterra–Cantor set an example of a closed set whose boundary has positive Lebesgue measure.

Other fat Cantor sets

In general, one can remove r_n from each remaining subinterval at the n-th step of the algorithm, and end up with a Cantor-like set. The resulting set will have positive measure if and only if the sum of the sequence is less than the measure of the initial interval. If the middle interval of length 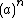is removed from 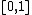for each n-th iteration, where 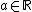this holds if and only if : the complement of the set obtained in this manner has Lebesgue measure

Hence the set itself has positive measure if and only if

Cartesian products of Smith–Volterra–Cantor sets can be used to find totally disconnected sets in higher dimensions with nonzero measure. By applying the Denjoy–Riesz theorem to a two-dimensional set of this type, it is possible to find a Jordan curve such that the points on the curve have positive area.^[2]

References

1. ^Aliprantis and Burkinshaw (1981), Principles of Real Analysis
2. ^{{citation | last1 = Balcerzak | first1 = M. | last2 = Kharazishvili | first2 = A. | doi = 10.1023/A:1022102312024 | issue = 3 | journal = Georgian Mathematical Journal | mr = 1679442 | pages = 201–212 | title = On uncountable unions and intersections of measurable sets | volume = 6 | year = 1999}}.

External links

Wrestling with the Fundamental Theorem of Calculus: Volterra's function, talk by David Marius Bressoud

4 : Sets of real numbers|Measure theory|Topological spaces|Fractals

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Construction

Properties

Other fat Cantor sets

See also

References

External links