“Minimum rank of a graph”的意思、由来-开放百科全书

词条

Minimum rank of a graph

释义

Definition
Properties
Characterization of known graph families
Notes
References

In mathematics, the minimum rank is a graph parameter for any graph G. It was motivated by the Colin de Verdière's invariant.

Definition

The adjacency matrix of a given undirected graph is a symmetric matrix whose rows and columns both correspond to the vertices of the graph. Its coefficients are all 0 or 1, and the coefficient in row i and column j is nonzero whenever vertex i is adjacent to vertex j in the graph. More generally, one can define a generalized adjacency matrix to be any matrix of real numbers with the same pattern of nonzeros. The minimum rank of the graph is denoted by and is defined as the smallest rank of any generalized adjacency matrix of the graph.

Properties

The minimum rank of a graph is always at most equal to n − 1, where n is the number of vertices in the graph.^[1]
For every induced subgraph H of a given graph G, the minimum rank of H is at most equal to the minimum rank of G.^[2]
If a given graph is not connected, then its minimum rank is the sum of the minimum ranks of its connected components.^[3]
The minimum rank is a graph invariant: any two isomorphic graphs necessarily have the same minimum rank.

Characterization of known graph families

Several families of graphs may be characterized in terms of their minimum ranks.

For 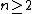, the complete graph K_n on n vertices has minimum rank one. The only graphs that are connected and have minimum rank one are the complete graphs.^[4]
A path graph P_n on n vertices has minimum rank n − 1. The only n-vertex graphs with minimum rank n − 1 are the path graphs.^[5]
A cycle graph C_n on n vertices has minimum rank n − 2.^[6]
Let be a 2-connected graph. Then if and only if is a linear 2-tree.^[7]
A graph has 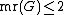if and only if the complement of is of the form for appropriate nonnegative integers 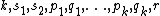with for all .^[8]

Notes

1. ^Fallat-Hogben, Observation 1.2.
2. ^Fallat-Hogben, Observation 1.6.
3. ^Fallat-Hogben, Observation 1.6.
4. ^Fallat-Hogben, Observation 1.2.
5. ^Fallat-Hogben, Corollary 1.5.
6. ^Fallat-Hogben, Observation 1.6.
7. ^Fallat-Hogben, Theorem 2.10.
8. ^Fallat-Hogben, Theorem 2.9.

References

{{citation

| last1 = Fallat | first1 = Shaun
| last2 = Hogben | first2 = Leslie
| contribution = The minimum rank of symmetric matrices described by a graph: A survey
| pages = 558–582
| title = Linear Algebra and its Applications 426 (2007)
| url = http://orion.math.iastate.edu/lhogben/research/FallatHogbenMinRank07.pdf}}.{{DEFAULTSORT:Minimum rank of a graph}}

2 : Algebraic graph theory|Graph invariants

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。