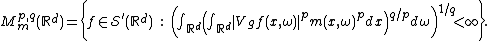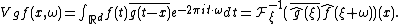- Feichtinger's algebra
- References
Modulation spaces[1] are a family of Banach spaces defined by the behavior of the short-time Fourier transform with
respect to a test function from the Schwartz space. They were originally proposed by Hans Georg Feichtinger and are recognized to be the right kind of function spaces for time-frequency analysis. Feichtinger's algebra, while originally introduced as a new Segal algebra,[2] is identical to a certain modulation space and has become a widely used space of test functions for time-frequency analysis.
Modulation spaces are defined as follows. For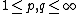 
, a non-negative function 
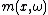on 
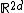and a test function 
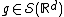, the modulation space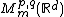 
is defined by
In the above equation,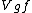 
denotes the short-time Fourier transform of 
with respect to 
evaluated at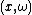 
, namely
In other words,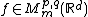 
is equivalent to 
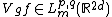. The space 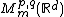is the same, independent of the test function 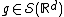chosen. The canonical choice is a Gaussian.
We also have a Besov-type definition of modulation spaces as follows.[3]
,
where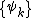 
is a suitable unity partition. If 
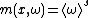, then 
.
Feichtinger's algebra
For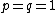 
and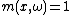 
, the modulation space 
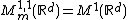is known by the name Feichtinger's algebra and often denoted by 
for being the minimal Segal algebra invariant under time-frequency shifts, i.e. combined translation and modulation operators.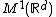 
is a Banach space embedded in 
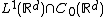, and is invariant under the Fourier transform. It is for these and more properties that 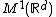is a natural choice of test function space for time-frequency analysis. Fourier transform 
is an automorphism on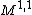 
.
References
2. ^H. Feichtinger. "On a new Segal algebra" Monatsh. Math. 92:269–289, 1981.
3. ^B.X. Wang, Z.H. Huo, C.C. Hao, and Z.H. Guo. [https://books.google.com/books?id=11O6CgAAQBAJ&printsec=frontcover#v=onepage&q&f=false Harmonic Analysis Method for Nonlinear Evolution Equations]. World Scientific, 2011.
- Zelezne Dveri
- Zeleznia
- Zeleznica
- Zeleznica, Greater Poland Voivodeship
- Zeleznica, Lodz Voivodeship
- Zeleznica, Lubusz Voivodeship
- Zeleznicar Belgrade
- Zeleznicar Beograd
- Zeleznica, Swietokrzyskie Voivodeship
- Zeleznice
- Zeleznice Slovenskej republiky
- Zeleznice Srbije
- Zeleznicka Kolonija
- Zeleznicna spolocnost Slovensko
- Zeleznik Belgrade
- Zeleznik Hall
- Zeleznik (horse)
- Zelezniki (disambiguation)
- Zelezniki, Lower Silesian Voivodeship
- Zelezniki, Masovian Voivodeship
- Zelezniki, Metlika
- Zeleznikowa Mala
- Zeleznikowa Wielka
- Zelezniska Postaja
- Zelezniski Muzej/Railway Museum