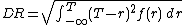“Sortino ratio”的意思、由来-开放百科全书

词条

Sortino ratio

释义

Definition
Usage
See also
References

The Sortino ratio measures the risk-adjusted return of an investment asset, portfolio, or strategy.^[1] It is a modification of the Sharpe ratio but penalizes only those returns falling below a user-specified target or required rate of return, while the Sharpe ratio penalizes both upside and downside volatility equally. Though both ratios measure an investment's risk-adjusted return, they do so in significantly different ways that will frequently lead to differing conclusions as to the true nature of the investment's return-generating efficiency.

The Sortino ratio is used as a way to compare the risk-adjusted performance of programs with differing risk and return profiles. In general, risk-adjusted returns seek to normalize the risk across programs and then see which has the higher return unit per risk.^[2]

Definition

The ratio is calculated as

,

where is the asset or portfolio average realized return, 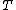is the target or required rate of return for the investment strategy under consideration (originally called the minimum acceptable return MAR), and 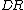is the target semi-deviation (the square root of target semi-variance), termed downside deviation. is expressed in percentages and therefore allows for rankings in the same way as standard deviation.

An intuitive way to view downside risk is the annualized standard deviation of returns below the target. Another is the square root of the probability-weighted squared below-target returns. The squaring of the below-target returns has the effect of penalizing failures at a quadratic rate. This is consistent with observations made on the behavior of individual decision making under uncertainty.

Here

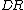= downside deviation or (commonly known in the financial community) "downside risk" (by extension, 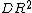= downside variance),

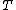= the annual target return, originally termed the minimum acceptable return MAR,

= the random variable representing the return for the distribution of annual returns 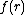, and

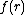= the distribution for the annual returns, e.g., the three-parameter lognormal distribution.

For the reasons provided below, this continuous formula is preferred over a simpler discrete version that determines the standard deviation of below-target periodic returns taken from the return series.

The continuous form permits all subsequent calculations to be made using annual returns, the natural way for investors to specify their investment goals. The discrete form requires monthly returns for there to be sufficient data points to make a meaningful calculation, which in turn requires converting the annual target into a monthly target. This significantly affects the amount of risk that is identified. For example, a goal of earning 1% in every month of one year results in a greater risk than the seemingly equivalent goal of earning 12% in one year.
A second reason for strongly preferring the continuous form to the discrete form has been proposed by Sortino & Forsey (1996):

"Before we make an investment, we don't know what the outcome will be... After the investment is made, and we want to measure its performance, all we know is what the outcome was, not what it could have been. To cope with this uncertainty, we assume that a reasonable estimate of the range of possible returns, as well as the probabilities associated with estimation of those returns...In statistical terms, the shape of [this] uncertainty is called a probability distribution. In other words, looking at just the discrete monthly or annual values does not tell the whole story."

Using the observed points to create a distribution is a staple of conventional performance measurement. For example, monthly returns are used to calculate a fund's mean and standard deviation. Using these values and the properties of the normal distribution, we can make statements such as the likelihood of losing money (even though no negative returns may actually have been observed) or the range within which two-thirds of all returns lies (even though the specific returns identifying this range have not necessarily occurred). Our ability to make these statements comes from the process of assuming the continuous form of the normal distribution and certain of its well-known properties.

In post-modern portfolio theory an analogous process is followed.

Observe the monthly returns.
Fit a distribution that permits asymmetry to the observations.
Annualize the monthly returns, making sure the shape characteristics of the distribution are retained.
Apply integral calculus to the resultant distribution to calculate the appropriate statistics.

As a caveat, some practitioners have fallen into the habit of using discrete periodic returns to compute downside risk. This method is conceptually and operationally incorrect and negates the foundational statistic of post-modern portfolio theory as developed by Brian M. Rom and Frank A. Sortino.

Usage

The Sortino ratio is used to score a portfolio's risk-adjusted returns relative to an investment target using downside risk. This is analogous to the Sharpe ratio, which scores risk-adjusted returns relative to the risk-free rate using standard deviation. When return distributions are near symmetrical and the target return is close to the distribution median, these two measure will produce similar results. As skewness increases and targets vary from the median, results can be expected to show dramatic differences.

References

1. ^{{cite journal |last=Sortino |first=F.A. |last2=Price |first2=L.N. |title=Performance measurement in a downside risk framework |year=1994 |journal=Journal of Investing |volume=3 |pages=50–8}}
2. ^{{cite web|url=http://www.redrockcapital.com/Sortino__A__Sharper__Ratio_Red_Rock_Capital.pdf |accessdate=February 16, 2014 |title=Sortino: A ‘Sharper’ Ratio|publisher=Red Rock Capital}}

3 : Financial ratios|Statistical ratios|Portfolio theories

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Definition

Usage

See also

References