1. Names of the sporadic groups

2. Organization
    I. Pariah  II. Happy Family  First generation (5 groups): the Mathieu groups  Second generation (7 groups): the Leech lattice  Third generation (8 groups): other subgroups of the Monster 

3. Table of the sporadic group orders

4. References

5. External links

In group theory, a sporadic group is one of the 26 exceptional groups found in the classification of finite simple groups.

A simple group is a group G that does not have any normal subgroups except for the trivial group and G itself. The classification theorem states that the list of finite simple groups consists of 18 countably infinite families, plus 26 exceptions that do not follow such a systematic pattern. These are the sporadic groups. They are also known as the sporadic simple groups, or the sporadic finite groups. Because it is not strictly a group of Lie type, the Tits group is sometimes regarded as a sporadic group,^[1] in which case the sporadic groups number 27.

The monster group is the largest of the sporadic groups and contains all but six of the other sporadic groups as subgroups or subquotients.

Names of the sporadic groups

Five of the sporadic groups were discovered by Mathieu in the 1860s and the other 21 were found between 1965 and 1975. Several of these groups were predicted to exist before they were constructed. Most of the groups are named after the mathematician(s) who first predicted their existence. The full list is:

• Mathieu groups M₁₁, M₁₂, M₂₂, M₂₃, M₂₄
• Janko groups J₁, J₂ or HJ, J₃ or HJM, J₄
• Conway groups Co₁, Co₂, Co₃
• Fischer groups Fi₂₂, Fi₂₃, Fi₂₄′ or F₃₊
• Higman–Sims group HS
• McLaughlin group McL
• Held group He or F₇₊ or F₇
• Rudvalis group Ru
• Suzuki group Suz or F₃₋
• O'Nan group O'N
• Harada–Norton group HN or F₅₊ or F₅
• Lyons group Ly
• Thompson group Th or F_3|3 or F₃
• Baby Monster group B or F₂₊ or F₂
• Fischer–Griess Monster group M or F₁

The Tits group T is sometimes also regarded as a sporadic group (it is almost but not strictly a group of Lie type), which is why in some sources the number of sporadic groups is given as 27 instead of 26.^[2] In some other sources, the Tits group is regarded as neither sporadic nor of Lie type.^[2] Anyway, it is the {{nowrap|(n{{=}}0)-member}} {{nowrap|²F₄(2)′}} of the infinite family of commutator groups {{nowrap|²F₄(2²ⁿ⁺¹)′,}} all of them finite simple groups. For n>0 they coincide with the groups of Lie type {{nowrap|²F₄(2²ⁿ⁺¹).}} But for {{nowrap|n{{=}}0,}} the derived subgroup {{nowrap|²F₄(2)′}}, called Tits group, has an index 2 in the group {{nowrap|²F₄(2)}} of Lie type.

Matrix representations over finite fields for all the sporadic groups have been constructed.

The earliest use of the term "sporadic group" may be {{harvtxt|Burnside|1911|loc=p. 504, note N}} where he comments about the Mathieu groups: "These apparently sporadic simple groups would probably repay a closer examination than they have yet received".

The diagram at right is based on {{Harvtxt|Ronan|2006}}. It does not show the numerous non-sporadic simple subquotients of the sporadic groups.

Organization

Of the 26 sporadic groups, 20 can be seen inside the Monster group as subgroups or quotients of subgroups (sections).

I. Pariah

The six exceptions are J₁, J₃, J₄, O'N, Ru and Ly. These six are sometimes known as the pariahs.

II. Happy Family

The remaining twenty have been called the Happy Family by Robert Griess, and can be organized into three generations.

First generation (5 groups): the Mathieu groups

M_n for n = 11, 12, 22, 23 and 24 are multiply transitive permutation groups on n points. They are all subgroups of M₂₄, which is a permutation group on 24 points.

Second generation (7 groups): the Leech lattice

All the subquotients of the automorphism group of a lattice in 24 dimensions called the Leech lattice:

• Co₁ is the quotient of the automorphism group by its center {±1}
• Co₂ is the stabilizer of a type 2 (i.e., length 2) vector
• Co₃ is the stabilizer of a type 3 (i.e., length {{radic|6}}) vector
• Suz is the group of automorphisms preserving a complex structure (modulo its center)
• McL is the stabilizer of a type 2-2-3 triangle
• HS is the stabilizer of a type 2-3-3 triangle
• J₂ is the group of automorphisms preserving a quaternionic structure (modulo its center).

Third generation (8 groups): other subgroups of the Monster

Consists of subgroups which are closely related to the Monster group M:

• B or F₂ has a double cover which is the centralizer of an element of order 2 in M
• Fi₂₄′ has a triple cover which is the centralizer of an element of order 3 in M (in conjugacy class "3A")
• Fi₂₃ is a subgroup of Fi₂₄′
• Fi₂₂ has a double cover which is a subgroup of Fi₂₃
• The product of Th = F₃ and a group of order 3 is the centralizer of an element of order 3 in M (in conjugacy class "3C")
• The product of HN = F₅ and a group of order 5 is the centralizer of an element of order 5 in M
• The product of He = F₇ and a group of order 7 is the centralizer of an element of order 7 in M.
• Finally, the Monster group itself is considered to be in this generation.

(This series continues further: the product of M₁₂ and a group of order 11 is the centralizer of an element of order 11 in M.)

The Tits group also belongs in this generation: there is a subgroup S₄ ײF₄(2)′ normalising a 2C² subgroup of B, giving rise to a subgroup

2·S₄ ײF₄(2)′ normalising a certain Q₈ subgroup of the Monster.

²F₄(2)′ is also a subgroup of the Fischer groups Fi₂₂, Fi₂₃ and Fi₂₄′, and of the Baby Monster B.

²F₄(2)′ is also a subgroup of the (pariah) Rudvalis group Ru, and has

no involvements in sporadic simple groups except the containments we have already mentioned.

Table of the sporadic group orders

Group	Generation	Order {{OEIS|id=A001228	1SF	Factorized order	Standard generators triple (a, b, ab)[3][4][5]	Further conditions
F1 or M	third	8080174247945128758864599049617107 57005754368000000000	53}}	246 · 320 · 59 · 76 · 112 · 133 · 17 · 19 · 23 · 29 · 31 · 41 · 47 · 59 · 71	2A, 3B, 29	none
F2 or B	third	4154781481226426191177580544000000	33}}	241 · 313 · 56 · 72 · 11 · 13 · 17 · 19 · 23 · 31 · 47	2C, 3A, 55
Fi24' or F3+	third	1255205709190661721292800	24}}	221 · 316 · 52 · 73 · 11 · 13 · 17 · 23 · 29	2A, 3E, 29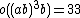
Fi23	third	4089470473293004800	18}}	218 · 313 · 52 · 7 · 11 · 13 · 17 · 23	2B, 3D, 28	none
Fi22	third	64561751654400	13}}	217 · 39 · 52 · 7 · 11 · 13	2A, 13, 11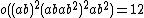
F3 or Th	third	90745943887872000	16}}	215 · 310 · 53 · 72 · 13 · 19 · 31	2, 3A, 19	none
Ly	pariah	51765179004000000	16}}	28 · 37 · 56 · 7 · 11 · 31 · 37 · 67	2, 5A, 14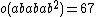
F5 or HN	third	273030912000000	14}}	214 · 36 · 56 · 7 · 11 · 19	2A, 3B, 22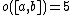
Co1	second	4157776806543360000	18}}	221 · 39 · 54 · 72 · 11 · 13 · 23	2B, 3C, 40	none
Co2	second	42305421312000	13}}	218 · 36 · 53 · 7 · 11 · 23	2A, 5A, 28	none
Co3	second	495766656000	11}}	210 · 37 · 53 · 7 · 11 · 23	2A, 7C, 17	none
O'N	pariah	460815505920	11}}	29 · 34 · 5 · 73 · 11 · 19 · 31	2A, 4A, 11	none
Suz	second	448345497600	11}}	213 · 37 · 52 · 7 · 11 · 13	2B, 3B, 13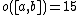
Ru	pariah	145926144000	11}}	214 · 33 · 53 · 7 · 13 · 29	2B, 4A, 13	none
F7 or He	third	4030387200	9}}	210 · 33 · 52 · 73 · 17	2A, 7C, 17	none
McL	second	898128000	8}}	27 · 36 · 53 · 7 · 11	2A, 5A, 11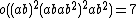
HS	second	44352000	7}}	29 · 32 · 53 · 7 · 11	2A, 5A, 11	none
J4	pariah	86775571046077562880	19}}	221 · 33 · 5 · 7 · 113 · 23 · 29 · 31 · 37 · 43	2A, 4A, 37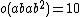
J3 or HJM	pariah	50232960	7}}	27 · 35 · 5 · 17 · 19	2A, 3A, 19
J2 or HJ	second	604800	5}}	27 · 33 · 52 · 7	2B, 3B, 7
J1	pariah	175560	5}}	23 · 3 · 5 · 7 · 11 · 19	2, 3, 7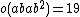
M24	first	244823040	8}}	210 · 33 · 5 · 7 · 11 · 23	2B, 3A, 23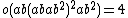
M23	first	10200960	7}}	27 · 32 · 5 · 7 · 11 · 23	2, 4, 23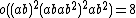
M22	first	443520	5}}	27 · 32 · 5 · 7 · 11	2A, 4A, 11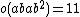
M12	first	95040	5}}	26 · 33 · 5 · 11	2B, 3B, 11	none
M11	first	7920	3}}	24 · 32 · 5 · 11	2, 4, 11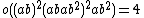

References

• {{citation |authorlink=William Burnside |first=William |last=Burnside |isbn=0-486-49575-2 |year=1911|title=Theory of groups of finite order |page=504 (note N)}}
• {{citation |authorlink=John Horton Conway |last=Conway |first=J. H. |title=A perfect group of order 8,315,553,613,086,720,000 and the sporadic simple groups |journal=Proc. Natl. Acad. Sci. U.S.A. |volume=61 |issue=2 |pages=398–400 |year=1968 |url=http://www.pnas.org/content/61/2/398.full.pdf+html |zbl=0186.32401 |doi=10.1073/pnas.61.2.398|pmc=225171 }}
• {{cite book |last=Conway |first=J. H. |last2=Curtis |first2=R. T. |author3link=Simon P. Norton |last3=Norton |first3=S. P. |last4=Parker |first4=R. A. |author5link=Robert Arnott Wilson |last5=Wilson |first5=R. A. |title=Atlas of finite groups. Maximal subgroups and ordinary characters for simple groups. With computational assistance from J. G. Thackray |publisher=Oxford University Press |year=1985 |isbn=0-19-853199-0 |zbl=0568.20001}}
• {{citation |authorlink=Daniel Gorenstein |first=D. |last=Gorenstein |author2link=Richard Lyons (mathematician) |first2=R. |last2=Lyons |author3link=Ronald Solomon |first3=R. |last3=Solomon |title=The Classification of the Finite Simple Groups |publisher=American Mathematical Society |year=1994 }} Issues 1, 2, ...
• {{citation |authorlink=R. L. Griess |last=Griess |first=Robert L. |title=Twelve Sporadic Groups |publisher=Springer-Verlag |year=1998 |isbn=3540627782 |zbl=0908.20007 |url=https://books.google.com/books?id=Ue2pJaegL50C}}
• {{Citation | last1=Ronan | first1=Mark | title=Symmetry and the Monster | publisher=Oxford | isbn=978-0-19-280722-9 | year=2006 | authorlink = Mark Ronan |zbl=1113.00002 |url=https://books.google.com/books?id=wDjD0PowhIwC }}

External links

• {{MathWorld|urlname=SporadicGroup|title=Sporadic Group}}
• Atlas of Finite Group Representations: Sporadic groups

• Tanana city school District
• Tanana Mission
• Tananam Tananam
• Tanana people
• Tanana peoples
• Tananarivo
• Tanana School District
• Tanana school district
• Tanana Valley State Fair
• Tananda
• Tan An province
• Tanant
• Tanaobela chrysochlora
• Tanaoctena collina
• Tanaoctena coptila
• Tanaoctena dubia
• Tanaoctena indubitata
• Tanaoctena ooptila
• Tanaoctena pygmaeodes
• Tanaoctenia haliaria
• Tanaoctenota dubia
• Tanaophysa adornatalis
• Tanaophysa rufiscripta
• Tanaophysopsis xanthyalinalis
• Tanaorhinus discolor