1. References

In topology, a branch of mathematics, a nilpotent space, first defined by E.Dror (1969),^[1] is a based topological space X such that

• the fundamental group 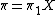is a nilpotent group;
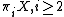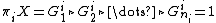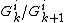• acts nilpotently^[2] on higher homotopy groups , i.e. there is a central series such that the induced action of on the quotient is trivial for all .

Simply connected spaces and simple spaces are (trivial) examples of nilpotent spaces, other examples are connected loop spaces. The homotopy fibre of

any map between nilpotent spaces is a disjoint union of nilpotent spaces, the null component of the pointed mapping space Map_*(K,X) where K is a pointed finite dimensional CW complex and X is any pointed space, is a nilpotent space. The odd-dimensional real projective spaces are nilpotent spaces, while the projective plane is not. A basic theorem about nilpotent spaces ^[3]states that any map that induces an integral homology isomorphism between two nilpotent space is a weak homotopy equivalence. Nilpotent spaces are of great interest in rational homotopy theory, because most constructions applicable to simply connected spaces can be extended to nilpotent spaces. The Bousfield Kan nilpotent completion of a space associates with any connected pointed space X a universal space X^ through which any map of X to a nilpotent space N factors uniquely up to contractible space of choices, often however, X^ itself is not nilpotent but only an inverse limit of a tower of nilpotent spaces. This tower, as a pro-space, always models the homology type of the given pointed space X. Nilpotent spaces admit a good arithmetic localization theory in the sense of Bousfield and Kan cited above, and the unstable Adams spectral sequence strongly converges

for any such space.

Let X be a nilpotent space and let h be a reduced generalized homology theory, such as K-theory.

If h(X)=0, then h vanishes on any Postnikov section of X. This follows from a theorem that states that

any such section is X-cellular.

References

• 509 BCE
• 509 (disambiguation)
• 509 Howard Street
• 509 in Ireland
• 509 Iolanda
• 509 (number)
• 509th
• 509th Bombardment Group
• 509th Bomb Group
• 509th Bomb Wing
• 509th Composite Group
• 509th Infantry Regiment
• 509th Operations Group
• 509th Parachute Infantry Battalion
• 509th Parachute Infantry Regiment
• 509th Security Forces Squadron
• 50 American Revolutions That You're Not Supposed To Know
• 50 Aquarii
• 50 B.C.
• .50 Beowulf
• 50 billion cent
• 50 Biscayne
• .50BMG
• 50 Bootis
• 50 Boötis