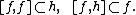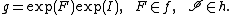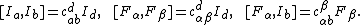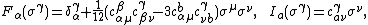1. See also

2. References

In mathematical physics, nonlinear realization of a Lie group G possessing a Cartan subgroup H is a particular induced representation of G. In fact, it is a representation of a Lie algebra of G in a neighborhood of its origin.

A nonlinear realization, when restricted to the subgroup H reduces to a linear representation.

A nonlinear realization technique is part and parcel of many field theories with spontaneous symmetry breaking, e.g., chiral models, chiral symmetry breaking, Goldstone boson theory, classical Higgs field theory, gauge gravitation theory and supergravity.

Let G be a Lie group and H its Cartan subgroup which admits a linear representation in a vector space V. A Lie

algebra of G splits into the sum 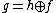of the Cartan subalgebra of H and its supplement 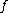, such that

(In physics, for instance, amount to vector generators and 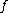to axial ones.)

There exists an open neighborhood U of the unit of G such

that any element 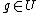is uniquely brought into the form

Let 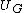be an open neighborhood of the unit of G such that

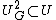, and let 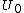be an open neighborhood of the

H-invariant center of the quotient G/H which consists of elements

Then there is a local section 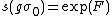of

over .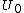

With this local section, one can define the induced representation, called the nonlinear realization, of elements 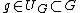on 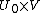given by the expressions

The corresponding nonlinear realization of a Lie algebra

of G takes the following form.

Let 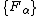, 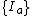be the bases for 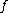and , respectively, together with the commutation relations

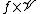Then a desired nonlinear realization of in reads

,

up to the second order in .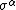

In physical models, the coefficients 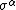are treated as Goldstone fields. Similarly, nonlinear realizations of Lie superalgebras are considered.

See also

• Induced representation
• Chiral model

References

• Coleman S., Wess J., Zumino B., Structure of phenomenological Lagrangians, I, II, Phys. Rev. 177 (1969) 2239.
• Joseph A., Solomon A., Global and infinitesimal nonlinear chiral transformations, J. Math. Phys. 11 (1970) 748.
• Giachetta G., Mangiarotti L., Sardanashvily G., Advanced Classical Field Theory, World Scientific, 2009, {{ISBN|978-981-283-895-7}}.

• Dehnow, Fars
• Deh Now, Fars
• Deh Now, Faryab
• Dehnow, Fathabad
• Deh Now, Fazl
• Deh Now, Firuzabad
• Deh Now, Gonabad
• Deh Now, Hajjiabad
• Deh Now, Hamadan
• Dehnow, Hamadan
• Deh Now, Harsin
• Deh Now, Hendijan
• Deh Now, Hormozgan
• Dehnow, Hormozgan
• Deh Now, Isfahan
• Deh Nowiyeh
• Dehnowiyeh
• Dehnow'iyeh
• Deh Now'iyeh
• Deh Nowiyeh (disambiguation)
• Deh Nowiyeh, Kuhbanan
• Dehnowiyeh, Ravar
• Deh Nowiyeh, Yazd
• Dehnowiyeh, Yazdanabad
• Dehnowiyeh, Zarand