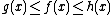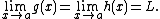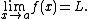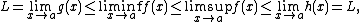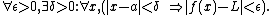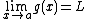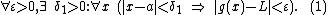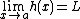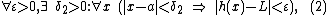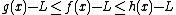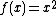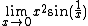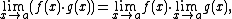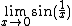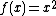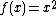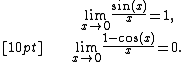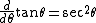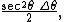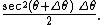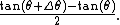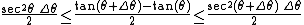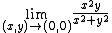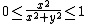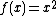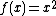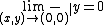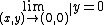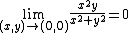“Squeeze theorem”的意思、由来-开放百科全书

词条

Squeeze theorem

释义

Statement
Proof
Statement for series
Proof
Examples
First example Second example Third example Fourth example
References
External links

{{Redirect|Sandwich theorem|the result in measure theory|Ham sandwich theorem}}

In calculus, the squeeze theorem, also known as the pinching theorem, the sandwich theorem, the sandwich rule, and sometimes the squeeze lemma, is a theorem regarding the limit of a function.

The squeeze theorem is used in calculus and mathematical analysis. It is typically used to confirm the limit of a function via comparison with two other functions whose limits are known or easily computed. It was first used geometrically by the mathematicians Archimedes and Eudoxus in an effort to compute {{pi}}, and was formulated in modern terms by Carl Friedrich Gauss.

In many languages (e.g. French, German, Italian and Russian), the squeeze theorem is also known as the two policemen (and a drunk) theorem, or some variation thereof.{{citation needed|date=February 2018}} The story is that if two policemen are escorting a drunk prisoner between them, and both officers go to a cell, then (regardless of the path taken, and the fact that the prisoner may be wobbling about between the policemen) the prisoner must also end up in the cell.

Statement

The squeeze theorem is formally stated as follows.^[1]

Let I be an interval having the point a as a limit point. Let g, f, and h be functions defined on I, except possibly at a itself. Suppose that for every x in I not equal to a, we have

and also suppose that

Then

The functions and are said to be lower and upper bounds (respectively) of .
Here, is not required to lie in the interior of . Indeed, if is an endpoint of , then the above limits are left- or right-hand limits.
A similar statement holds for infinite intervals: for example, if 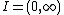, then the conclusion holds, taking the limits as .

This theorem is also valid for sequences. Let 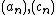be two sequences converging to , and a sequence. If 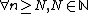we have 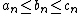, then also converges to .

Proof

From the above hypotheses we have, taking the limit inferior and superior:

so all the inequalities are indeed equalities, and the thesis immediately follows.

A direct proof, using the 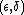-definition of limit, would be to prove that for all real there exists a real such that for all with 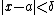, we have . Symbolically,

means that

and

means that

then we have

We can choose 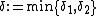. Then, if 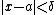, combining (1) and (2), we have

,

which completes the proof.

The proof for sequences is very similar, using the -definition of a limit of a sequence.

Statement for series

There is also the squeeze theorem for series, which can be stated as follows:{{cn|date=March 2018}}

Let be two convergent series. If such that then also converges.

Proof

Let 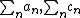be two convergent series. Hence, the sequences 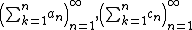are Cauchy. That is, for fixed ,

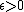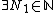such that 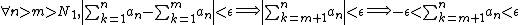(1)

and similarly 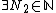such that 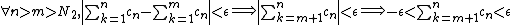(2).

We know that 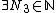such that 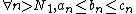. Hence, 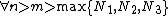, we have combining (1) and (2):

Therefore 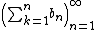is a Cauchy sequence. So 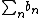converges.

Examples

First example

The limit

cannot be determined through the limit law

because

does not exist.

However, by the definition of the sine function,

It follows that

Since 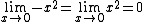, by the squeeze theorem, 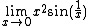must also be 0.

Second example

Probably the best-known examples of finding a limit by squeezing are the proofs of the equalities

The first limit follows by means of the squeeze theorem from the fact that

^[2]

for x close enough to 0. The correctness of which for positive x can be seen by simple geometric reasoning (see drawing) that can be extended to negative x as well. The second limit follows from the squeeze theorem and the fact that

for x close enough to 0. This can be derived by replacing in the earlier fact by 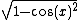and squaring the resulting inequality.

These two limits are used in proofs of the fact that the derivative of the sine function is the cosine function. That fact is relied on in other proofs of derivatives of trigonometric functions.

Third example

It is possible to show that

by squeezing, as follows.

In the illustration at right, the area of the smaller of the two shaded sectors of the circle is

since the radius is sec θ and the arc on the unit circle has length Δθ. Similarly, the area of the larger of the two shaded sectors is

What is squeezed between them is the triangle whose base is the vertical segment whose endpoints are the two dots. The length of the base of the triangle is tan(θ + Δθ) − tan(θ), and the height is 1. The area of the triangle is therefore

From the inequalities

we deduce that

provided Δθ > 0, and the inequalities are reversed if Δθ < 0. Since the first and third expressions approach sec²θ as Δθ → 0, and the middle expression approaches (d/dθ) tan θ, the desired result follows.

Fourth example

The squeeze theorem can still be used in multivariable calculus but the lower (and upper functions) must be below (and above) the target function not just along a path but around the entire neighborhood of the point of interest and it only works if the function really does have a limit there. It can, therefore, be used to prove that a function has a limit at a point, but it can never be used to prove that a function does not have a limit at a point.^[3]

cannot be found by taking any number of limits along paths that pass through the point, but since

therefore, by the squeeze theorem,

References

1. ^{{cite book|last1=Sohrab|first1=Houshang H.|title=Basic Real Analysis|date=2003|publisher=Birkhäuser|isbn=978-1-4939-1840-9|page=104|edition=2nd|url=https://books.google.com/books?id=QnpqBQAAQBAJ&pg=PA104}}
2. ^Selim G. Krejn, V.N. Uschakowa: Vorstufe zur höheren Mathematik. Springer, 2013, {{ISBN|9783322986283}}, pp. [https://books.google.de/books?id=-yXMBgAAQBAJ&pg=PA80 80-81] (German). See also Sal Khan: [https://www.khanacademy.org/math/ap-calculus-ab/limits-from-equations-ab/squeeze-theorem-ab/v/proof-lim-sin-x-x Proof: limit of (sin x)/x at x=0] (video, Khan Academy)
3. ^{{cite book|chapter=Chapter 15.2 Limits and Continuity|pages=909–910|title=Multivariable Calculus|year=2008|last1=Stewart|first1=James|authorlink1=James_Stewart_(mathematician)|edition=6th|isbn=0495011630}}

External links

{{MathWorld |title=Squeezing Theorem |urlname=SqueezingTheorem}}
Squeeze Theorem by Bruce Atwood (Beloit College) after work by, Selwyn Hollis (Armstrong Atlantic State University), the Wolfram Demonstrations Project.
[https://proofwiki.org/wiki/Squeeze_Theorem Squeeze Theorem] on Proofs.wiki.

5 : Limits (mathematics)|Functions and mappings|Articles containing proofs|Theorems in calculus|Theorems in real analysis

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。