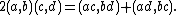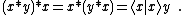“Okubo algebra”的意思、由来-开放百科全书

词条

Okubo algebra

释义

Construction of Para-Hurwitz algebra
Scalar product Involution in Hurwitz algebras Para-Hurwitz algebra
References

In algebra, an Okubo algebra or pseudo-octonion algebra is an 8-dimensional non-associative algebra similar to the one studied by Susumu Okubo ^[1]. Okubo algebras are composition algebras, flexible algebras (A(BA) = (AB)A), Lie admissible algebras, and power associative, but are not associative, not alternative algebras, and do not have an identity element.

Okubo's example was the algebra of 3 by 3 trace zero complex matrices, with the product of X and Y given by aXY + bYX – Tr(XY)I/3 where I is the identity matrix and a and b satisfy a + b = 3ab = 1. The Hermitian elements form an 8-dimensional real non-associative division algebra. A similar construction works for any cubic alternative separable algebra over a field containing a primitive cube root of unity. An Okubo algebra is an algebra constructed in this way from the trace 0 elements of a degree 3 central simple algebra over a field.^[2]

Construction of Para-Hurwitz algebra

Unital composition algebras are called Hurwitz algebras.^[3]{{rp|22}} If the ground field {{math|1=K}} is the field of real numbers and {{mvar|N}} is positive-definite, then {{mvar|A}} is called a Euclidean Hurwitz algebra.

Scalar product

If {{mvar|K}} has characteristic not equal to 2, then a bilinear form {{math|1=(a, b) = {{sfrac|1|2}}[N(a + b) − N(a) − N(b)]}} is associated with the quadratic form {{mvar|N}}.

Involution in Hurwitz algebras

Assuming {{mvar|A}} has a multiplicative unity, define involution and right and left multiplication operators by

Evidently {{overline| }} is an involution and preserves the quadratic form. The overline notation stresses the fact that complex and quaternion conjugation are partial cases of it. These operators have the following properties:

The involution is an antiautomorphism, i.e. {{math|1={{overline|a b}} = {{overline|b}} {{overline|a}}}}
{{math|1=a {{overline|a}} = N(a) 1 = {{overline|a}} a}}
{{math|1=L({{overline|a}}) = L(a)}}, {{math|1=R({{overline|a}}) = R(a)}}, where {{math|}} denotes the adjoint operator with respect to the form {{math|( , )}}
{{math|1=Re(a b) = Re(b a)}} where {{math|1=Re x = (x + {{overline|x}})/2 = (x, 1)}}
{{math|1=Re((a b) c) = Re(a (b c))}}
{{math|1=L(a²) = L(a)²}}, {{math|1=R(a²) = R(a)²}}, so that {{mvar|A}} is an alternative algebra

These properties are proved starting from polarized version of the identity {{math|1=(a b, a b) = (a, a)(b, b)}}:

Setting {{math|1=b = 1}} or {{math|1=d = 1}} yields {{math|1=L({{overline|a}}) = L(a)*}} and {{math|1=R({{overline|c}}) = R(c)*}}. Hence {{math|1=Re(a b) = (a b, 1) = (a, {{overline|b}}) = (b a, 1) = Re(b a)}}. Similarly {{math|1=({{overline|a b}}, c) = (a b, {{overline|c}}) = (b, {{overline|a}} {{overline|c}}) = (1, {{overline|b}} ({{overline|a}} {{overline|c}})) = (1, ({{overline|b}} {{overline|a}}) {{overline|c}}) = ({{overline|b}} {{overline|a}}, c)}}. Hence {{math|1=Re(a b)c = ((a b)c, 1) = (a b, {{overline|c}}) = (a, {{overline|c}} {{overline|b}}) = (a(b c), 1) = Re(a(b c))}}. By the polarized identity {{math|1=N(a) (c, d) = (a c, a d) = ({{overline|a}} a c, d)}} so {{math|1=L({{overline|a}}) L(a) = N(a)}}. Applied to 1 this gives {{math|1={{overline|a}} a = N(a)}}. Replacing {{mvar|a}} by {{overline|a|class=texhtml}} gives the other identity. Substituting the formula for {{math|{{overline|a}}}} in {{math|1=L({{overline|a}}) L(a) = L({{overline|a}} a)}} gives {{math|1=L(a)² = L(a²)}}.

Para-Hurwitz algebra

Another operation {{math|∗}} may be defined in a Hurwitz algebra as

{{math|1=x ∗ y = {{overline|x}} {{overline|y}}}}

The algebra {{math|(A, ∗)}} is a composition algebra not generally unital, known as a para-Hurwitz algebra.^[2]{{rp|484}} In dimensions 4 and 8 these are para-quaternion^[4] and para-octonion algebras.^[3]{{rp|40,41}}

A para-Hurwitz algebra satisfies^[3]{{rp|48}}

Conversely, an algebra with a non-degenerate symmetric bilinear form satisfying this equation is either a para-Hurwitz algebra or an eight-dimensional pseudo-octonion algebra.^[3]{{rp|49}} Similarly, a flexible algebra satisfying

is either a Hurwitz algebra, a para-Hurwitz algebra or an eight-dimensional pseudo-octonion algebra.^[3]

References

1. ^{{harvs|txt|first=Susumu|last=Okubo|year=1978}}
2. ^¹Max-Albert Knus, Alexander Merkurjev, Markus Rost, Jean-Pierre Tignol (1998) "Composition and Triality", chapter 8 in The Book of Involutions, pp 451–511, Colloquium Publications v 44, American Mathematical Society {{isbn|0-8218-0904-0}}
3. ^¹²³⁴{{cite book | zbl=0841.17001 | last=Okubo | first=Susumu | title=Introduction to octonion and other non-associative algebras in physics | series=Montroll Memorial Lecture Series in Mathematical Physics | volume=2 | location=Cambridge | publisher=Cambridge University Press | year=1995 | isbn=0-521-47215-6 |url=https://books.google.com/books?id=Tr3qQugHUvQC |mr=1356224}}
4. ^The term "para-quaternions" is sometimes applied to unrelated algebras.

{{eom|id=Okubo_algebra}}
{{citation

|last=Okubo |first=Susumu
|year=1978
|title=Pseudo-quaternion and pseudo-octonion algebras
|journal=Hadronic Journal
|volume=1 |issue= 4|pages=1250–1278
|mr=0510100
}}

Susumu Okubo & J. Marshall Osborn (1981) "Algebras with nondegenerate associative symmetric bilinear forms permitting composition", Communications in Algebra 9(12): 1233–61, {{mr|id=0618901}} and 9(20): 2015–73 {{mr|id=0640611}}.

2 : Composition algebras|Non-associative algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。