- Symmetry
- Images
- Related polytopes and honeycombs Rectified order-5 hexagonal tiling honeycomb Truncated order-5 hexagonal tiling honeycomb Cantellated order-5 hexagonal tiling honeycomb Bitruncated order-5 hexagonal tiling honeycomb Cantitruncated order-5 hexagonal tiling honeycomb Runcinated order-5 hexagonal tiling honeycomb Runcitruncated order-5 hexagonal tiling honeycomb Omnitruncated order-5 hexagonal tiling honeycomb
- See also
- References
| Order-5 hexagonal tiling honeycomb | |
|---|---|
Perspective projection view from center of Poincaré disk model | |
| Type | Hyperbolic regular honeycomb Paracompact uniform honeycomb |
| Schläfli symbol | {6,3,5} |
| Coxeter-Dynkin diagrams | node_1|6|node|3|node|5|node}} ↔ {{CDD|node_1|6|node_g|3sg|node_g|5g|node_g}} |
| Cells | {6,3} |
| Faces | hexagon {6} |
| Edge figure | pentagon {5} |
| Vertex figure | {3,5} |
| Dual | Order-6 dodecahedral honeycomb |
| Coxeter group | HV}}3, [6,3,5] |
| Properties | Regular |
In the field of hyperbolic geometry, the order-5 hexagonal tiling honeycomb arises one of 11 regular paracompact honeycombs in 3-dimensional hyperbolic space. It is called paracompact because it has infinite cells. Each cell consists of a hexagonal tiling whose vertices lie on a horosphere: a flat plane in hyperbolic space that approaches a single ideal point at infinity.
The Schläfli symbol of the order-5 hexagonal tiling honeycomb is {6,3,5}. Since that of the hexagonal tiling of the plane is {6,3}, this honeycomb has five such hexagonal tilings meeting at each edge. Since the Schläfli symbol of the icosahedron is {3,5}, the vertex figure of this honeycomb is an icosahedron. Thus, 20 hexagonal tilings meet at each vertex of this honeycomb.[1]
{{Honeycomb}}Symmetry
A lower symmetry, [6,(3,5)*], index 120 construction exists with regular dodecahedral fundamental domains, and an icosahedral shaped Coxeter diagram with 6 axial infinite order (ultraparallel) branches.
Images
It is similar to the 2D hyperbolic regular tiling, {∞,5}, with infinite apeirogonal faces, and 5 meeting around every vertex (peak).
Related polytopes and honeycombs
It is one of 15 regular hyperbolic honeycombs in 3-space, 11 of which like this one are paracompact, with infinite cells or vertex figures.
{{Regular_paracompact_H3_honeycombs}}There are 15 uniform honeycombs in the [5,3,6] Coxeter group family, including this regular form and its regular dual, order-5 hexagonal tiling honeycomb, {6,3,5}.
{{635 family}}It has a related alternation honeycomb, represented by {{CDD|node_h1|6|node|3|node|5|node}} ↔ {{CDD|branch_10ru|split2|node|5|node}}, having icosahedron and triangular tiling cells.
It is a part of sequence of regular honeycombs with hexagonal tiling hyperbolic honeycombs of the form {6,3,p}:
{{Hexagonal tiling cell tessellations}}This honeycomb is a part of a sequence of polychora and honeycombs with icosahedron vertex figures:
{{Icosahedral vertex figure tessellations}}Rectified order-5 hexagonal tiling honeycomb
| Rectified order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbols | r{6,3,5} or t1{6,3,5} 2r{5,3[3]} |
| Coxeter diagrams | node|6|node_1|3|node|5|node}} {{CDD|node_h0|6|node_1|3|node|5|node}} ↔ {{CDD|branch_11|split2|node|5|node}} |
| Cells | {3,5} r{6,3}, r{3[3]} |
| Faces | Triangle {3} Pentagon {5} Hexagon {6} |
| Vertex figure | Pentagonal prism {}×{5} |
| Coxeter groups | 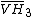 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive, edge-transitive |
The rectified order-5 hexagonal tiling honeycomb, t1{6,3,5}, {{CDD|node|6|node_1|3|node|5|node}} has icosahedron and trihexagonal tiling facets, with a pentagonal prism vertex figure.
It is similar to the 2D hyperbolic infinite-order square tiling, r{∞,5} with pentagon and apeirogonal faces. All vertices are on the ideal surface.
{{Pentagonal prism vertex figure tessellations}}{{-}}Truncated order-5 hexagonal tiling honeycomb
| Truncated order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t{6,3,5} or t0,1{6,3,5} |
| Coxeter diagram | node_1|6|node_1|3|node|5|node}} |
| Cells | {3,5} t{6,3} |
| Faces | Triangle {3} Pentagon {5} Hexagon {6} |
| Vertex figure | Pentagonal pyramid {}v{5} |
| Coxeter groups | 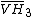 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive |
The truncated order-5 hexagonal tiling honeycomb, t0,1{6,3,5}, {{CDD|node_1|6|node_1|3|node|5|node}} has icosahedron and triangular tiling facets, with a pentagonal pyramid vertex figure.
{{-}}Cantellated order-5 hexagonal tiling honeycomb
| Cantellated order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | rr{6,3,5} or t0,2{6,3,5} |
| Coxeter diagram | node_1|6|node|3|node_1|5|node}} |
| Cells | r{3,5} rr{6,3} |
| Faces | Triangle {3} Pentagon {5} Hexagon {6} |
| Vertex figure | triangular prism |
| Coxeter groups | 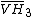 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive |
The cantellated order-5 hexagonal tiling honeycomb, t0,2{6,3,5}, {{CDD|node_1|6|node|3|node_1|5|node}} has icosidodecahedron and rhombitrihexagonal tiling facets, with a triangular prism vertex figure.
{{-}}Bitruncated order-5 hexagonal tiling honeycomb
| Bitruncated order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | 2t{6,3,5} or t1,2{6,3,5} |
| Coxeter diagram | node|6|node_1|3|node_1|5|node}} |
| Cells | |
| Faces | |
| Vertex figure | Tetrahedron |
| Coxeter groups | 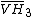 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive |
The bitruncated order-5 hexagonal tiling honeycomb, t1,2{6,3,5}, {{CDD|node|6|node_1|3|node_1|5|node}} has a tetrahedral vertex figure.
{{-}}Cantitruncated order-5 hexagonal tiling honeycomb
| Cantitruncated order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | tr{6,3,5} or t0,1,2{6,3,5} |
| Coxeter diagram | node_1|6|node_1|3|node_1|5|node}} |
| Cells | t{3,5} tr{6,3} |
| Faces | Pentagon {5} Hexagon {6} Dodecagon {12} |
| Vertex figure | triangular prism |
| Coxeter groups | 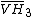 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive |
The cantitruncated order-5 hexagonal tiling honeycomb, t0,1,2{6,3,5}, {{CDD|node_1|6|node_1|3|node_1|5|node}} has truncated icosahedron and truncated trihexagonal tiling facets, with a tetrahedral vertex figure.
{{-}}Runcinated order-5 hexagonal tiling honeycomb
| Runcinated order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t0,3{6,3,5} |
| Coxeter diagram | node_1|6|node|3|node|5|node_1}} |
| Cells | |
| Faces | |
| Vertex figure | triangular antiprism |
| Coxeter groups | 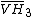 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive |
The runcinated order-5 hexagonal tiling honeycomb, t0,3{6,3,5}, {{CDD|node_1|6|node|3|node|5|node_1}} has dodecahedron and truncated trihexagonal tiling facets, with a triangular antiprism vertex figure.
{{-}}Runcitruncated order-5 hexagonal tiling honeycomb
| Runcitruncated order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t0,1,3{6,3,5} |
| Coxeter diagram | node_1|6|node_1|3|node|5|node_1}} |
| Cells | |
| Faces | |
| Vertex figure | trapezoidal pyramid |
| Coxeter groups | 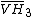 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive |
The runcitruncated order-5 hexagonal tiling honeycomb, t0,1,3{6,3,5}, {{CDD|node_1|6|node_1|3|node|5|node_1}} has a trapezoidal pyramid vertex figure.
{{-}}Omnitruncated order-5 hexagonal tiling honeycomb
| Omnitruncated order-5 hexagonal tiling honeycomb | |
|---|---|
| Type | Paracompact uniform honeycomb |
| Schläfli symbol | t0,1,2,3{6,3,5} |
| Coxeter diagram | node_1|6|node_1|3|node_1|5|node_1}} |
| Cells | |
| Faces | |
| Vertex figure | tetrahedron |
| Coxeter groups | 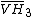 , [6,3,5] , [6,3,5] |
| Properties | Vertex-transitive |
The omnitruncated order-5 hexagonal tiling honeycomb, t0,1,2,3{6,3,5}, {{CDD|node_1|6|node_1|3|node_1|5|node_1}} has a tetrahedral vertex figure.
{{-}}See also
- Convex uniform honeycombs in hyperbolic space
- List of regular polytopes
References
- Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. {{isbn|0-486-61480-8}}. (Tables I and II: Regular polytopes and honeycombs, pp. 294–296)
- The Beauty of Geometry: Twelve Essays (1999), Dover Publications, {{LCCN|99035678}}, {{isbn|0-486-40919-8}} (Chapter 10, Regular Honeycombs in Hyperbolic Space) Table III
- Jeffrey R. Weeks The Shape of Space, 2nd edition {{isbn|0-8247-0709-5}} (Chapter 16-17: Geometries on Three-manifolds I,II)
- Norman Johnson Uniform Polytopes, Manuscript
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- N.W. Johnson: Geometries and Transformations, (2018) Chapter 13: Hyperbolic Coxeter groups
- Eucalyptus formanii
- Eucalyptus fracta
- Eucalyptus fraseri
- Eucalyptus froggattii
- Eucalyptus fruticosa
- Eucalyptus fulgens
- Eucalyptus fusiformis
- Eucalyptus gamophylla
- Eucalyptus gardneri
- Eucalyptus georgei
- Eucalyptus gigantangion
- Eucalyptus gilbertensis
- Eucalyptus gillenii
- Eucalyptus gittinsii
- Eucalyptus glaucina
- Eucalyptus glomericassis
- Eucalyptus glomerosa
- Eucalyptus gongylocarpa
- Eucalyptus goniantha
- Eucalyptus goniocarpa
- Eucalyptus gonyocalyx
- Eucalyptus gracilis
- Eucalyptus grandifolia
- Eucalyptus granitica
- Eucalyptus grasbyi