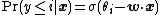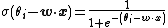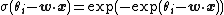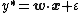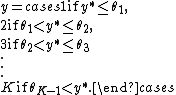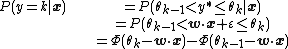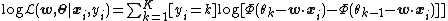1. Linear models for ordinal regression
    Latent variable model 

2. Alternative models

3. Software

4. See also

5. Notes

6. References

7. Further reading

In statistics, ordinal regression (also called "ordinal classification") is a type of regression analysis used for predicting an ordinal variable, i.e. a variable whose value exists on an arbitrary scale where only the relative ordering between different values is significant. It can be considered an intermediate problem between regression and classification^[1][2]. Examples of ordinal regression are ordered logit and ordered probit. Ordinal regression turns up often in the social sciences, for example in the modeling of human levels of preference (on a scale from, say, 1–5 for "very poor" through "excellent"), as well as in information retrieval. In machine learning, ordinal regression may also be called ranking learning.^[3]{{efn|Not to be confused with learning to rank.}}

Linear models for ordinal regression

Ordinal regression can be performed using a generalized linear model (GLM) that fits both a coefficient vector and a set of thresholds to a dataset. Suppose one has a set of observations, represented by length-{{mvar|p}} vectors {{math|x₁}} through {{math|x_n}}, with associated responses {{math|y₁}} through {{mvar|y_n}}, where each {{mvar|y_i}} is an ordinal variable on a scale {{math|1, ..., K}}. For simplicity, and without loss of generality, we assume {{mvar|y}} is a non-decreasing vector, that is, {{mvar|1=y_i y_i+1}}. To this data, one fits a length-{{mvar|p}} coefficient vector {{math|w}} and a set of thresholds {{math|θ₁, ..., θ_K−1}} with the property that {{math|θ₁ < θ₂ < ... < θ_K−1}}. This set of thresholds divides the real number line into {{mvar|K}} disjoint segments, corresponding to the {{mvar|K}} response levels.

The model can now be formulated as

or, the cumulative probability of the response {{mvar|y}} being at most {{mvar|i}} is given by a function {{mvar|σ}} (the inverse link function) applied to a linear function of {{math|x}}. Several choices exist for {{mvar|σ}}; the logistic function

gives the ordered logit model, while using the probit function gives the ordered probit model. A third option is to use an exponential function

which gives the proportional hazards model.^[4]

Latent variable model

The probit version of the above model can be justified by assuming the existence of a real-valued latent variable (unobserved quantity) {{mvar|y*}}, determined by^[5]

where {{mvar|ε}} is normally distributed with zero mean and unit variance, conditioned on {{math|x}}. The response variable {{mvar|y}} results from an "incomplete measurement" of {{mvar|y*}}, where one only determines the interval into which {{mvar|y*}} falls:

Defining {{math|θ₀ {{=}} -∞}} and {{math|θ_K {{=}} ∞}}, the above can be summarized as {{math|y {{=}} k}} if and only if {{math|θ_k−1 < y* ≤ θ_k}}.

From these assumptions, one can derive the conditional distribution of {{mvar|y}} as{{r|wooldridge}}

where {{math|Φ}} is the cumulative distribution function of the standard normal distribution, and takes on the role of the inverse link function {{mvar|σ}}. The log-likelihood of the model for a single training example {{math|x_i}}, {{mvar|y_i}} can now be stated as{{r|wooldridge}}

(using the Iverson bracket {{math|[y_i {{=}} k]}}.) The log-likelihood of the ordered logit model is analogous, using the logistic function instead of {{math|Φ}}.^[6]

Alternative models

In machine learning, alternatives to the latent-variable models of ordinal regression have been proposed. An early result was PRank, a variant of the perceptron algorithm that found multiple parallel hyperplanes separating the various ranks; its output is a weight vector {{math|w}} and a sorted vector of {{math|K−1}} thresholds {{math|θ}}, as in the ordered logit/probit models. The prediction rule for this model is to output the smallest rank {{mvar|k}} such that {{math|wx < θ_k}}.^[7]

Other methods rely on the principle of large-margin learning that also underlies support vector machines.^[8][9]

Another approach is given by Rennie and Srebro, who, realizing that "even just evaluating the likelihood of a predictor is not straight-forward" in the ordered logit and ordered probit models, propose fitting ordinal regression models by adapting common loss functions from classification (such as the hinge loss and log loss) to the ordinal case.^[10]

Software

ORCA (Ordinal Regression and Classification Algorithms) is a Octave/MATLAB framework including a wide set of ordinal regression methods^[11].

See also

• Logistic regression

Notes

References

Further reading

• {{cite book | last = Agresti | first = Alan | title = Analysis of ordinal categorical data | publisher = Wiley | location = Hoboken, N.J | year = 2010 | isbn = 978-0470082898 }}
• {{cite book |last=Greene |first=William H. |authorlink=William Greene (economist) |title=Econometric Analysis |edition=Seventh |location=Boston |publisher=Pearson Education |year=2012 |isbn=978-0-273-75356-8 |pages=824–842 }}
• {{cite book |last=Hardin |first=James |last2=Hilbe |first2=Joseph |authorlink2=Joseph Hilbe |title=Generalized Linear Models and Extensions |publisher=College Station: Stata Press |date=2007 |edition=2nd | isbn=978-1-59718-014-6}}

• Rybka 3 Aquarium
• Rybka 4
• Rybka (disambiguation)
• Rybka (film)
• Rybka Lututowska
• Rybka Sokolska
• Rybki
• Rybkin
• Rybna
• Rybna (disambiguation)
• Rybna, Lesser Poland Voivodeship
• Rybna nad Zdobnici
• Rybna, Opole Voivodeship
• Rybna, Silesian Voivodeship
• Rybne
• Rybne, Masovian Voivodeship
• Rybne, Podkarpackie Voivodeship
• Rybnica (disambiguation)
• Rybnica, Jelenia Gora County
• Rybnica Lesna
• Rybnica Leśna
• Rybnica, Lublin Voivodeship
• Rybnica-Niwka
• Rybnica, Swietokrzyskie Voivodeship
• Rybnica, West Pomeranian Voivodeship