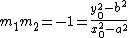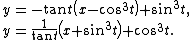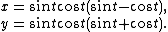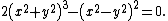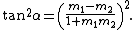请输入您要查询的百科知识：

　

词条 Orthoptic (geometry)
释义

  1. Orthoptic of a parabola

  2. Orthoptic of an ellipse and hyperbola

      Ellipse    Hyperbola  

  3. Orthoptic of an astroid

  4. Isoptic of a parabola, an ellipse and a hyperbola

      Equations of the isoptics    Proofs  

  5. External links

  6. Notes

  7. References

{{For|the branch of medicine|Orthoptics}}

In the geometry of curves, an orthoptic is the set of points for which two tangents of a given curve meet at a right angle.

Examples:

  1. The orthoptic of a parabola is its directrix (proof: see below),
  2. The orthoptic of an ellipse {{math|{{sfrac|x2|a2}} + {{sfrac|y2|b2}} {{=}} 1}} is the director circle {{math|x2 + y2 {{=}} a2 + b2}} (see below),
  3. The orthoptic of a hyperbola {{math|{{sfrac|x2|a2}} − {{sfrac|y2|b2}} {{=}} 1}}, {{math|a > b}}, is the circle {{math|x2 + y2 {{=}} a2 − b2}} (in case of {{math|a ≤ b}} there are no orthogonal tangents, see below),
  4. The orthoptic of an astroid {{math|x{{frac|2|3}} + y{{frac|2|3}} {{=}} 1}} is a quadrifolium with the polar equation

(see below).

Generalizations:

  1. An isoptic is the set of points for which two tangents of a given curve meet at a fixed angle (see below).
  2. An isoptic of two plane curves is the set of points for which two tangents meet at a fixed angle.
  3. Thales' theorem on a chord {{mvar|PQ}} can be considered as the orthoptic of two circles which are degenerated to the two points {{mvar|P}} and {{mvar|Q}}.

Orthoptic of a parabola

Any parabola can be transformed by a rigid motion (angles are not changed) into a parabola with equation 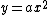. The slope at a point of the parabola is 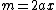. Replacing gives the parametric representation of the parabola with the tangent slope as parameter: The tangent has the equation with the still unknown , which can be determined by inserting the coordinates of the parabola point. One gets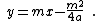

If a tangent contains the point {{math|(x0, y0)}}, off the parabola, then the equation

holds, which has two solutions {{math|m1}} and {{math|m2}} corresponding to the two tangents passing {{math|(x0, y0)}}. The free term of a reduced quadratic equation is always the product of its solutions. Hence, if the tangents meet at {{math|(x0, y0)}} orthogonally, the following equations hold:

The last equation is equivalent to

which is the equation of the directrix.

Orthoptic of an ellipse and hyperbola

Ellipse

{{main|Director circle}}

Let be the ellipse of consideration.

(1) The tangents of ellipse at neighbored vertices intersect at one of the 4 points , which lie on the desired orthoptic curve (circle ).

(2) The tangent at a point of the ellipse has the equation (s. Ellipse). If the point is not a vertex this equation can be solved: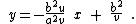

Using the abbreviations and the equation one gets:

Hence and the equation of a non vertical tangent is

Solving relations for and respecting leads to the slope depending parametric representation of the ellipse:

(For an other proof: see Ellipse.)

If a tangent contains the point , off the ellipse, then the equation

holds. Eliminating the square root leads to

which has two solutions corresponding to the two tangents passing . The free term of a reduced quadratic equation is always the product of its solutions. Hence, if the tangents meet at orthogonally, the following equations hold:

The last equation is equivalent to

From (1) and (2) one gets:

  • The intersection points of orthogonal tangents are points of the circle .

Hyperbola

The ellipse case can be adopted nearly exactly to the hyperbola case. The only changes to be made are to replace with 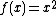and to restrict {{mvar|m}} to {{math|{{abs|m}} > {{sfrac|b|a}}}}. Therefore:

  • The intersection points of orthogonal tangents are points of the circle , where {{math|a > b}}.

Orthoptic of an astroid

An astroid can be described by the parametric representation

.

From the condition

one recognizes the distance {{mvar|α}} in parameter space at which an orthogonal tangent to {{math|{{vec|ċ}}(t)}} appears. It turns out that the distance is independent of parameter {{mvar|t}}, namely {{math|α {{=}} ± {{sfrac|π|2}}}}. The equations of the (orthogonal) tangents at the points {{math|{{vec|c}}(t)}} and {{math|{{vec|c}}(t + {{sfrac|π|2}})}} are respectively:

Their common point has coordinates:

This is simultaneously a parametric representation of the orthoptic.

Elimination of the parameter {{mvar|t}} yields the implicit representation

Introducing the new parameter {{math|φ {{=}} t − {{sfrac|5π|4}}}} one gets

(The proof uses the angle sum and difference identities.) Hence we get the polar representation

of the orthoptic. Hence:

  • The orthoptic of an astroid is a quadrifolium.

Isoptic of a parabola, an ellipse and a hyperbola

Below the isotopics for angles {{math|α ≠ 90°}} are listed. They are called {{mvar|α}}-isoptics. For the proofs see below.

Equations of the isoptics

Parabola

The {{mvar|α}}-isoptics of the parabola with equation {{math|y {{=}} ax2}} are the branches of the hyperbola

The branches of the hyperbola provide the isoptics for the two angles {{mvar|α}} and {{mvar|180° − α}} (see picture).

Ellipse

The {{mvar|α}}-isoptics of the ellipse with equation {{math|{{sfrac|x2|a2}} + {{sfrac|y2|b2}} {{=}} 1}} are the two parts of the degree-4 curve

(see picture).

Hyperbola

The {{mvar|α}}-isoptics of the hyperbola with the equation {{math|{{sfrac|x2|a2}} − {{sfrac|y2|b2}} {{=}} 1}} are the two parts of the degree-4 curve

Proofs

Parabola

A parabola {{math|y {{=}} ax2}} can be parametrized by the slope of its tangents {{math|m {{=}} 2ax}}:

The tangent with slope {{mvar|m}} has the equation

The point {{math|(x0, y0)}} is on the tangent if and only if

This means the slopes {{math|m1}}, {{math|m2}} of the two tangents containing {{math|(x0, y0)}} fulfil the quadratic equation

If the tangents meet at angle {{mvar|α}} or {{math|180° − α}}, the equation

must be fulfilled. Solving the quadratic equation for {{mvar|m}}, and inserting {{math|m1}}, {{math|m2}} into the last equation, one gets

This is the equation of the hyperbola above. Its branches bear the two isoptics of the parabola for the two angles {{mvar|α}} and {{math|180° − α}}.

Ellipse

In the case of an ellipse {{math|{{sfrac|x2|a2}} + {{sfrac|y2|b2}} {{=}} 1}} one can adopt the idea for the orthoptic for the quadratic equation

Now, as in the case of a parabola, the quadratic equation has to be solved and the two solutions {{math|m1}}, {{math|m2}} must be inserted into the equation

Rearranging shows that the isoptics are parts of the degree-4 curve:

Hyperbola

The solution for the case of a hyperbola can be adopted from the ellipse case by replacing {{math|b2}} with {{math|−b2}} (as in the case of the orthoptics, see above).

To visualize the isoptics, see implicit curve.

External links

{{commons category|Isoptics}}
  • Special Plane Curves.
  • Mathworld
  • Jan Wassenaar's Curves
  • "Isoptic curve" at MathCurve
  • "Orthoptic curve" at MathCurve

Notes

References

  • {{cite book | first=J. Dennis|last= Lawrence | title=A catalog of special plane curves | publisher=Dover Publications | year=1972 | isbn=0-486-60288-5 | pages=58–59 }}
  • {{cite journal|first=Boris|last= Odehnal |title=Equioptic Curves of Conic Sections |journal=Journal for Geometry and Graphics| volume=14 |date=2010 |issue=1 |page= 29–43}}
  • {{cite journal|first=Hermann |last=Schaal |title=Lineare Algebra und Analytische Geometrie |volume=III |publisher=Vieweg |date=1977 |ISBN=3-528-03058-5 |page=220}}
  • {{cite book|first=Jacob |last=Steiner |title=Vorlesungen über synthetische Geometrie |publisher=B. G. Teubner |location=Leipzig |date=1867 |url=https://books.google.com/books?id=jCgPAAAAQAAJ |at= Part 2, p. 186}}
  • {{cite journal|first=Maurizio|last= Ternullo|title=Two new sets of ellipse related concyclic points|journal=Journal of Geometry |date=2009 |volume=94 |page=159–173}}
{{Differential transforms of plane curves}}

1 : Curves
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/9/22 16:50:40