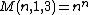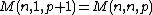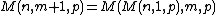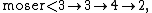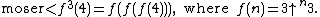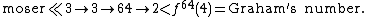“Steinhaus–Moser notation”的意思、由来-开放百科全书

词条

Steinhaus–Moser notation

释义

Definitions
Special values
Mega
Moser's number
See also
References
External links

In mathematics, Steinhaus–Moser notation is a notation for expressing certain extremely large numbers. It is an extension of Steinhaus's polygon notation.^[1]

Definitions

a number {{math|n}} in a triangle means {{math|nⁿ}}.

a number {{math|n}} in a square is equivalent to "the number {{math|n}} inside {{math|n}} triangles, which are all nested."

a number {{math|n}} in a pentagon is equivalent with "the number {{math|n}} inside {{math|n}} squares, which are all nested."

etc.: {{math|n}} written in an ({{math|m + 1}})-sided polygon is equivalent with "the number {{math|n}} inside {{math|n}} nested {{math|m}}-sided polygons". In a series of nested polygons, they are associated inward. The number {{math|n}} inside two triangles is equivalent to {{math|nⁿ}} inside one triangle, which is equivalent to {{math|nⁿ}} raised to the power of {{math|nⁿ}}.

Steinhaus defined only the triangle, the square, and the circle , which is equivalent to the pentagon defined above.

Special values

Steinhaus defined:

mega is the number equivalent to 2 in a circle: {{h:title|C(2) = S(S(2))|②}}
megiston is the number equivalent to 10 in a circle: ⑩

Moser's number is the number represented by "2 in a megagon", where a megagon is a polygon with "mega" sides, not to be confused with the megagon, with one million sides.

Alternative notations:

use the functions square(x) and triangle(x)
let {{math|M(n, m, p)}} be the number represented by the number {{math|n}} in {{math|m}} nested {{math|p}}-sided polygons; then the rules are:
and
- mega =
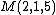
- megiston =
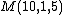
- moser =

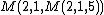
Mega

A mega, ②, is already a very large number, since ② =

square(square(2)) = square(triangle(triangle(2))) =

square(triangle(2²)) =

square(triangle(4)) =

square(4⁴) =

square(256) =

triangle(triangle(triangle(...triangle(256)...))) [256 triangles] =

triangle(triangle(triangle(...triangle(256²⁵⁶)...))) [255 triangles] ~

triangle(triangle(triangle(...triangle(3.2 × 10⁶¹⁶)...))) [254 triangles] =

...

Using the other notation:

mega = M(2,1,5) = M(256,256,3)

With the function 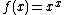we have mega = 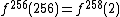where the superscript denotes a functional power, not a numerical power.

We have (note the convention that powers are evaluated from right to left):

M(256,2,3) =
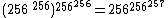
M(256,3,3) = ≈

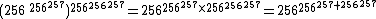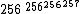
Similarly:

M(256,4,3) ≈
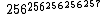
M(256,5,3) ≈

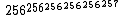
etc.

Thus:

mega = 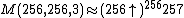, where 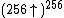denotes a functional power of the function .

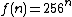Rounding more crudely (replacing the 257 at the end by 256), we get mega ≈ 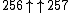, using Knuth's up-arrow notation.

After the first few steps the value of is each time approximately equal to 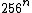. In fact, it is even approximately equal to 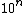(see also approximate arithmetic for very large numbers). Using base 10 powers we get:

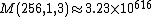
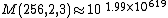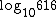( is added to the 616)
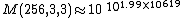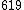( is added to the 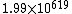, which is negligible; therefore just a 10 is added at the bottom)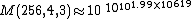

...

mega = 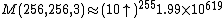, where 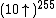denotes a functional power of the function . Hence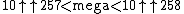

Moser's number

It has been proven that in Conway chained arrow notation,

and, in Knuth's up-arrow notation,

Therefore, Moser's number, although incomprehensibly large, is vanishingly small compared to Graham's number:

References

1. ^Hugo Steinhaus, Mathematical Snapshots, Oxford University Press 1969³, {{ISBN|0195032675}}, pp. 28-29

External links

Robert Munafo's Large Numbers
Factoid on Big Numbers
Megistron at mathworld.wolfram.com (Note that Steinhaus referred to this number as "megiston" with no "r".)
Circle notation at mathworld.wolfram.com

2 : Mathematical notation|Large numbers

随便看