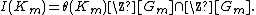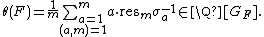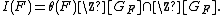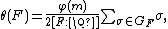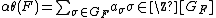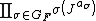“Stickelberger's theorem”的意思、由来-开放百科全书

词条

Stickelberger's theorem

释义

The Stickelberger element and the Stickelberger ideal
Examples
Statement of the theorem
See also
Notes
References
External links

In mathematics, Stickelberger's theorem is a result of algebraic number theory, which gives some information about the Galois module structure of class groups of cyclotomic fields. A special case was first proven by Ernst Kummer (Kummer|1847}}|1847) while the general result is due to Ludwig Stickelberger (Stickelberger|1890}}|1890).^[1]

The Stickelberger element and the Stickelberger ideal

Let {{mvar|K_m}} denote the {{mvar|m}}th cyclotomic field, i.e. the extension of the rational numbers obtained by adjoining the {{mvar|m}}th roots of unity to {{math|ℚ}} (where {{math|m ≥ 2}} is an integer). It is a Galois extension of {{math|ℚ}} with Galois group {{mvar|G_m}} isomorphic to the multiplicative group of integers modulo {{mvar|m}} {{math|(ℤ/mℤ)^×}}. The Stickelberger element (of level {{mvar|m}} or of {{mvar|K_m}}) is an element in the group ring {{math|ℚ[G_m]}} and the Stickelberger ideal (of level {{mvar|m}} or of {{mvar|K_m}}) is an ideal in the group ring {{math|ℤ[G_m]}}. They are defined as follows. Let {{mvar|ζ_m}} denote a primitive {{mvar|m}}th root of unity. The isomorphism from {{math|(ℤ/mℤ)^×}} to {{mvar|G_m}} is given by sending {{mvar|a}} to {{mvar|σ_a}} defined by the relation

.

The Stickelberger element of level {{mvar|m}} is defined as

The Stickelberger ideal of level {{mvar|m}}, denoted {{math|I(K_m)}}, is the set of integral multiples of {{math|θ(K_m)}} which have integral coefficients, i.e.

More generally, if {{mvar|F}} be any Abelian number field whose Galois group over {{math|ℚ}} is denoted {{mvar|G_F}}, then the Stickelberger element of {{mvar|F}} and the Stickelberger ideal of {{mvar|F}} can be defined. By the Kronecker–Weber theorem there is an integer {{mvar|m}} such that {{mvar|F}} is contained in {{mvar|K_m}}. Fix the least such {{mvar|m}} (this is the (finite part of the) conductor of {{mvar|F}} over {{math|ℚ}}). There is a natural group homomorphism {{math|G_m → G_F}} given by restriction, i.e. if {{math|σ ∈ G_m}}, its image in {{mvar|G_F}} is its restriction to {{mvar|F}} denoted {{math|res_mσ}}. The Stickelberger element of {{mvar|F}} is then defined as

The Stickelberger ideal of {{mvar|F}}, denoted {{math|I(F)}}, is defined as in the case of {{mvar|K_m}}, i.e.

In the special case where {{math|F {{=}} K_m}}, the Stickelberger ideal {{math|I(K_m)}} is generated by {{math|(a − σ_a)θ(K_m)}} as {{mvar|a}} varies over {{math|ℤ/mℤ}}. This not true for general F.^[2]

Examples

If {{mvar|F}} is a totally real field of conductor {{mvar|m}}, then^[3]

where {{mvar|φ}} is the Euler totient function and {{math|[F : ℚ]}} is the degree of {{mvar|F}} over ℚ.

Statement of the theorem

Stickelberger's Theorem^[4]
Let {{mvar|F}} be an abelian number field. Then, the Stickelberger ideal of {{mvar|F}} annihilates the class group of {{mvar|F}}.

Note that {{math|θ(F)}} itself need not be an annihilator, but any multiple of it in {{math|ℤ[G_F]}} is.

Explicitly, the theorem is saying that if {{math|α ∈ ℤ[G_F]}} is such that

and if {{mvar|J}} is any fractional ideal of {{mvar|F}}, then

is a principal ideal.

Notes

1. ^{{harvnb|Washington|1997|loc=Notes to chapter 6}}
2. ^{{harvnb|Washington|1997}}, Lemma 6.9 and the comments following it
3. ^{{harvnb|Washington|1997|loc=§6.2}}
4. ^{{harvnb|Washington|1997|loc=Theorem 6.10}}

References

{{cite book |last=Cohen |first=Henri |authorlink= Henri Cohen (number theorist) | year=2007 | title=Number Theory – Volume I: Tools and Diophantine Equations | isbn= 978-0-387-49922-2 | publisher=Springer-Verlag | series=Graduate Texts in Mathematics | volume=239| zbl=1119.11001 | pages=150–170 }}
Boas Erez, Darstellungen von Gruppen in der Algebraischen Zahlentheorie: eine Einführung
{{cite book | zbl=0376.12002 | last=Fröhlich | first=A. | author-link=Albrecht Fröhlich | chapter=Stickelberger without Gauss sums | pages=589–607 | title=Algebraic Number Fields, Proc. Symp. London Math. Soc., Univ. Durham 1975 | editor1-last=Fröhlich | editor1-first=A. | editor1-link=Albrecht Fröhlich | publisher=Academic Press | year=1977 | isbn=0-12-268960-7 }}
{{cite book | last1=Ireland | first1=Kenneth | last2=Rosen | first2=Michael | title=A Classical Introduction to Modern Number Theory | place=New York | edition=2nd | publisher=Springer-Verlag | series = Graduate Texts in Mathematics | volume=84 | year=1990 | isbn=978-1-4419-3094-1 | mr=1070716 | doi=10.1007/978-1-4757-2103-4}}
{{Citation

| last=Kummer
| first=Ernst
| author-link=Ernst Kummer
| title=Über die Zerlegung der aus Wurzeln der Einheit gebildeten complexen Zahlen in ihre Primfactoren
| year=1847
| journal=Journal für die Reine und Angewandte Mathematik
| volume=35
| pages=327–367
| doi=10.1515/crll.1847.35.327
}}

{{Citation

| last=Stickelberger
| first=Ludwig
| author-link=Ludwig Stickelberger
| title=Ueber eine Verallgemeinerung der Kreistheilung
| url=http://gdz.sub.uni-goettingen.de/no_cache/dms/load/img/?IDDOC=27547
| journal=Mathematische Annalen
| volume=37
| number=3
| year=1890
| pages=321–367
| mr=1510649 | jfm = 22.0100.01
| doi=10.1007/bf01721360
}}

{{Citation

| last=Washington
| first=Lawrence
| title=Introduction to Cyclotomic Fields
| edition=2
| publisher=Springer-Verlag
| location=Berlin, New York
| series=Graduate Texts in Mathematics
| isbn=978-0-387-94762-4
| mr=1421575
| year=1997
| volume=83
}}

External links

PlanetMath page

2 : Cyclotomic fields|Theorems in algebraic number theory

随便看