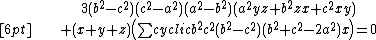“Parry point (triangle)”的意思、由来-开放百科全书

词条

Parry point (triangle)

释义

Parry circle
Parry point
See also
References
External links

In geometry, the Parry point is a special point associated with a plane triangle. It is a triangle center and it is called X(111) in Clark Kimberling's Encyclopedia of Triangle Centers. The Parry point is named in honor of the English geometer Cyril Parry, who studied them in the early 1990s.^[1]

Parry circle

Let ABC be a plane triangle. The circle through the centroid and the two isodynamic points of triangle ABC is called the Parry circle of triangle ABC. The equation of the Parry circle in barycentric coordinates is^[2]

The center of the Parry circle is also a triangle center. It is the center designated as X(351) in Encyclopedia of Triangle Centers. The trilinear coordinates of the center of the Parry circle are

f( a, b, c ) : f ( b , c, a ) : f ( c, a, b ), where f ( a , b, c ) = a ( b² − c² ) ( b² + c² − 2a² )

Parry point

The Parry circle and the circumcircle of triangle ABC intersect in two points. One of them is a focus of the Kiepert parabola of triangle ABC.^[3] The other point of intersection is called the Parry point of triangle ABC.

The trilinear coordinates of the Parry point are

( a / ( 2 a² − b² − c² ) : b / ( 2 b² − c² − a² ) : c / ( 2 c² − a² − b² ) )

The point of intersection of the Parry circle and the circumcircle of triangle ABC which is a focus of the Kiepert hyperbola of triangle ABC is also a triangle center and it is designated as X(110) in Encyclopedia of Triangle Centers. The trilinear coordinates of this triangle center are

( a / ( b² − c² ) : b / ( b² − a² ) : c / ( a² − b² ) )

References

1. ^{{cite web|last=Kimberling|first=Clark|title=Parry point|url=http://faculty.evansville.edu/ck6/tcenters/recent/parry.html|accessdate=29 May 2012}}
2. ^{{cite journal|last=Yiu|first=Paul|title=The Circles of Lester, Evans, Parry, and Their Generalizations|journal=Forum Geometricorum|year=2010|volume=10|pages=175–209|url=http://forumgeom.fau.edu/FG2010volume10/FG201020.pdf|accessdate=29 May 2012}}
3. ^{{cite web|last=Weisstein|first=Eric W|title=Parry Point|url=http://mathworld.wolfram.com/ParryPoint.html|publisher=MathWorld—A Wolfram Web Resource.|accessdate=29 May 2012}}

External links

1 : Triangle centers

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Parry circle

Parry point

See also

References

External links