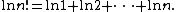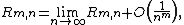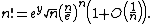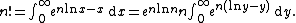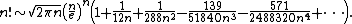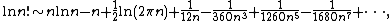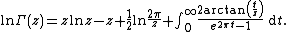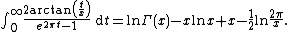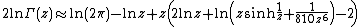1. Derivation

2. An alternative derivation

3. Speed of convergence and error estimates

4. Stirling's formula for the gamma function

5. Error bounds

6. A convergent version of Stirling's formula

7. Versions suitable for calculators

8. History

9. See also

10. Notes

11. References

12. External links

In mathematics, Stirling's approximation (or Stirling's formula) is an approximation for factorials. It is a good approximation, leading to accurate results even for small values of {{mvar|n}}. It is named after James Stirling, though it was first stated by Abraham de Moivre.^[1][2][3]

The version of the formula typically used in applications is

(in big O notation, as ), or, by changing the base of the logarithm (for instance in the worst-case lower bound for comparison sorting),

Specifying the constant in the {{math|O(ln n)}} error term gives {{math|{{sfrac|1|2}}ln(2πn)}}, yielding the more precise formula:

where the sign ~ means that the two quantities are asymptotic: their ratio tends to 1 as {{mvar|n}} tends to infinity.

One may also give simple bounds valid for all positive integers {{mvar|n}}, rather than only for large {{mvar|n}}:

for . These follow from the more precise error bounds discussed below.

Derivation

Roughly speaking, the simplest version of Stirling's formula can be quickly obtained by approximating the sum:

with an integral:

The full formula, together with precise estimates of its error, can be derived as follows. Instead of approximating {{math|n!}}, one considers its natural logarithm as this is a slowly varying function:

The right-hand side of this equation minus

is the approximation by the trapezoid rule of the integral

and the error in this approximation is given by the Euler–Maclaurin formula:

where {{mvar|B_k}} is a Bernoulli number and {{math|R_m,n}} is the remainder term in the Euler–Maclaurin formula. Take limits to find that

Denote this limit as {{mvar|y}}. Because the remainder {{math|R_m,n}} in the Euler–Maclaurin formula satisfies

where we use big-O notation, combining the equations above yields the approximation formula in its logarithmic form:

Taking the exponential of both sides, and choosing any positive integer {{mvar|m}}, we get a formula involving an unknown quantity {{mvar|e^y}}. For {{math|m {{=}} 1}}, the formula is

The quantity {{mvar|e^y}} can be found by taking the limit on both sides as {{mvar|n}} tends to infinity and using Wallis' product, which shows that {{math|e^y {{=}} {{sqrt|2π}}}}. Therefore, we get Stirling's formula:

An alternative derivation

An alternative formula for {{math|n!}} using the gamma function is

(as can be seen by repeated integration by parts). Rewriting and changing variables {{math|x {{=}} ny}} one gets

Applying Laplace's method we have:

which recovers Stirling's formula,

In fact further corrections can also be obtained using Laplace's method. For example, computing two-order expansion using Laplace's method yields

and gives Stirling's formula to two orders,

A complex-analysis version of this method^[4] is to consider as a Taylor coefficient of the exponential function 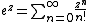, computed by Cauchy's integral formula as:

This line integral can then be approximated using the saddle point method with an appropriate choice of countour radius . The dominant portion of the integral near the saddle point is then approximated by a real integral and Laplace's method, while the remaining portion of the integral can be bounded above to give an error term.

Speed of convergence and error estimates

Stirling's formula is in fact the first approximation to the following series (now called the Stirling series^[5]):

An explicit formula for the coefficients in this series was given by G. Nemes.^[6]{{efn|Further terms are listed in the On-Line Encyclopedia of Integer Sequences as {{OEIS link|A001163}} and {{OEIS link|A001164}}.}} The first graph in this section shows the relative error vs. {{mvar|n}}, for 1 through all 5 terms listed above.

As {{math|n → ∞}}, the error in the truncated series is asymptotically equal to the first omitted term. This is an example of an asymptotic expansion. It is not a convergent series; for any particular value of {{mvar|n}} there are only so many terms of the series that improve accuracy, after which point accuracy actually gets worse. This is shown in the next graph, which shows the relative error versus the number of terms in the series, for larger numbers of terms. More precisely, let {{math|S(n, t)}} be the Stirling series to {{mvar|t}} terms evaluated at {{mvar|n}}. The graphs show

which, when small, is essentially the relative error.

Writing Stirling's series in the form

it is known that the error in truncating the series is always of the opposite sign and at most the same magnitude as the first omitted term.

More precise bounds, due to Robbins,^[7] valid for all positive integers {{mvar|n}} are

Stirling's formula for the gamma function

For all positive integers,

where {{math|Γ}} denotes the gamma function.

However, the gamma function, unlike the factorial, is more broadly defined for all complex numbers other than non-positive integers; nevertheless, Stirling's formula may still be applied. If {{math|Re(z) > 0}} then

Repeated integration by parts gives

where {{mvar|B_n}} is the {{mvar|n}}th Bernoulli number (note that the limit of the sum as is not convergent, so this formula is just an asymptotic expansion). The formula is valid for {{mvar|z}} large enough in absolute value when {{math|{{abs|arg(z)}} < π − ε}}, where {{mvar|ε}} is positive, with an error term of {{math|O(z^{−2N+ 1})}}. The corresponding approximation may now be written:

A further application of this asymptotic expansion is for complex argument {{mvar|z}} with constant {{math|Re(z)}}. See for example the Stirling formula applied in {{math|Im(z) {{=}} t}} of the Riemann-Siegel theta function on the straight line {{math|{{sfrac|1|4}} + it}}.

Error bounds

For any positive integer {{mvar|N}}, we introduce the following notation:

and

Then ^[8][9]

For further information and other error bounds, see the cited papers.

A convergent version of Stirling's formula

Thomas Bayes showed, in a letter to John Canton published by the Royal Society in 1763, that Stirling's formula did not give a convergent series.^[10] Obtaining a convergent version of Stirling's formula entails evaluating Raabe's formula:

One way to do this is by means of a convergent series of inverted rising exponentials. If

then

where

where {{math|s(n, k)}} denotes the Stirling numbers of the first kind. From this we obtain a version of Stirling's series

which converges when {{math|Re(x) > 0}}.

Versions suitable for calculators

The approximation

and its equivalent form

can be obtained by rearranging Stirling's extended formula and observing a coincidence between the resultant power series and the Taylor series expansion of the hyperbolic sine function. This approximation is good to more than 8 decimal digits for {{mvar|z}} with a real part greater than 8. Robert H. Windschitl suggested it in 2002 for computing the gamma function with fair accuracy on calculators with limited program or register memory.^[11]

Gergő Nemes proposed in 2007 an approximation which gives the same number of exact digits as the Windschitl approximation but is much simpler:^[12]

or equivalently,

An alternative approximation for the Gamma function stated by Srinivasa Ramanujan (Ramanujan 1988{{clarify|This is obviously supposed to be a citation but its target is not clear|date=May 2018}}) is

for {{math|x ≥ 0}}. The equivalent approximation for {{math|ln n!}} has an asymptotic error of {{math|{{sfrac|1|1400n³}}}} and is given by

The approximation may be made precise by giving paired upper and lower bounds; one such inequality is

^{[13][14][15][16]}

History

The formula was first discovered by Abraham de Moivre^[2] in the form

De Moivre gave an approximate rational-number expression for the natural logarithm of the constant. Stirling's contribution consisted of showing that the constant is precisely .^[3]

See also

• Factorial
• Gamma function
• Lanczos approximation
• Spouge's approximation

Notes

References

• {{citation |last=Olver |first=F. W. J. |last2= Olde Daalhuis |first2=A. B. |last3=Lozier |first3=D. W. |last4=Schneider |first4=B. I. |last5=Boisvert |first5=R. F. |last6=Clark |first6=C. W. |last7=Miller |first7=B. R. |last8=Saunders |first8=B. V. |lastauthoramp=yes |title=NIST Digital Library of Mathematical Functions |version=Release 1.0.13 of 2016-09-16 |url=http://dlmf.nist.gov/5.11}}
• {{citation |last=Abramowitz |first=M. |last2=Stegun |first2=I. |lastauthoramp=yes |title=Handbook of Mathematical Functions |year=2002 |url=http://www.math.hkbu.edu.hk/support/aands/toc.htm }}
• {{citation

• {{citation |last=Paris |first=R. B. |last2=Kaminski |first2=D. |lastauthoramp=yes |chapter= |title=Asymptotics and the Mellin–Barnes Integrals |year=2001 |publisher=Cambridge University Press |location=New York |isbn=978-0-521-79001-7 }}
• {{citation |last=Whittaker |first=E. T. |last2=Watson |first2=G. N. |lastauthoramp=yes |title=A Course in Modern Analysis |year=1996 |edition=4th |publisher=Cambridge University Press |location=New York |isbn=978-0-521-58807-2 }}
• Dan Romik, Stirling’s Approximation for n!: The Ultimate Short Proof?, The American Mathematical Monthly, Vol. 107, No. 6 (Jun. – Jul., 2000), 556–557.
• Y.-C. Li, A Note on an Identity of The Gamma Function and Stirling’s Formula, Real Analysis Exchang, Vol. 32(1), 2006/2007, pp. 267–272.

External links

• {{springer|title=Stirling formula|id=p/s087830}}
• Peter Luschny, Approximation formulas for the factorial function n!
• {{MathWorld | urlname=StirlingsApproximation | title=Stirling's Approximation}}
• {{PlanetMath | urlname=StirlingsApproximation | title=Stirling's approximation}}

• Pinus pallasiana
• Pinus pentophylla
• Pinus peregrinus
• Pinus pityusa
• Pinus polita
• Pinus sativa
• Pinus sect. Balfourinae
• Pinus torano
• Pinv
• Pinwale
• Pinwall
• Pin Wang
• Pin ware
• Pinware
• Pinware, Newfoundland and Labrador
• Pinwatta
• Pinwheel (disambiguation)
• Pinwheel eye
• Pinwheel Marasmius
• Pinwheel mushroom
• Pinwheel of death
• Pinwheels
• Pinwherry railway station
• Pinwinnie
• Pin worm