“Peeling theorem”的意思、由来-开放百科全书

词条

Peeling theorem

释义

References
External links

In general relativity, the peeling theorem describes the asymptotic behavior of the Weyl tensor as one goes to null infinity. Let be a null geodesic in a spacetime from a point p to null infinity, with affine parameter . Then the theorem states that, as tends to infinity:

where 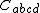is the Weyl tensor, and we used the abstract index notation. Moreover, in the Petrov classification, 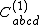is type N, 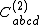is type III, 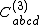is type II (or II-II) and 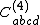is type I.

References

{{Citation

|last=Wald
|first=Robert M.
|title=General Relativity
|publisher=University of Chicago Press
|year=1984
|isbn=0-226-87033-2
}}

External links

[https://arxiv.org/abs/gr-qc/0505026]
[https://books.google.com/books?id=xIYpAQAAMAAJ&q=Peeling+theorem&dq=Peeling+theorem&hl=en&sa=X&ei=tkwBT9ugBqLQmAXj7fW_Dw&redir_esc=y]
[https://books.google.com/books?id=YP0-AAAAIAAJ&q=Peeling+theorem&dq=Peeling+theorem&hl=en&sa=X&ei=tkwBT9ugBqLQmAXj7fW_Dw&redir_esc=y]
[https://books.google.com/books?id=5xYvAAAAIAAJ&q=Peeling+theorem&dq=Peeling+theorem&hl=en&sa=X&ei=tkwBT9ugBqLQmAXj7fW_Dw&redir_esc=y]

2 : General relativity|Theorems in mathematical physics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。