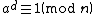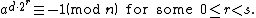- Formal definition
- Properties of strong pseudoprimes
- Examples
- Smallest strong pseudoprime to base n
- References
In number theory, a probable prime is a number that passes a primality test.
A strong probable prime is a number that passes a strong version of a primality test.
A strong pseudoprime is a composite number that passes a strong version of a primality test.
All primes pass these tests, but a small fraction of composites also pass, making them "false primes".
Unlike the Fermat pseudoprimes, for which there exist numbers that are pseudoprimes to all coprime bases (the Carmichael numbers), there are no composites that are strong pseudoprimes to all bases.
Formal definition
An odd composite number n = d · 2s + 1 where d is odd is called a strong (Fermat) pseudoprime to base a when one of the following conditions holds:
or
(If a number n satisfies one of the above conditions and we don't yet know whether it is prime, it is more precise to refer to it as a strong probable prime to base a. But if we know that n is not prime, then one may use the term strong pseudoprime.)
The definition is trivially met if {{math|a ≡ ±1 (mod n)}} so these trivial bases are often excluded.
Guy mistakenly gives a definition with only the first condition, which is not satisfied by all primes.[1]Properties of strong pseudoprimes
A strong pseudoprime to base a is always an Euler–Jacobi pseudoprime, an Euler pseudoprime [2] and a Fermat pseudoprime to that base, but not all Euler and Fermat pseudoprimes are strong pseudoprimes. Carmichael numbers may be strong pseudoprimes to some bases—for example, 561 is a strong pseudoprime to base 50—but not to all bases.
A composite number n is a strong pseudoprime to at most one quarter of all bases below n;[3][4] thus, there are no "strong Carmichael numbers", numbers that are strong pseudoprimes to all bases. Thus given a random base, the probability that a number is a strong pseudoprime to that base is less than 1/4, forming the basis of the widely used Miller–Rabin primality test.
However, Arnault
[5]gives a 397-digit Carmichael number that is a strong pseudoprime to every base less than 307.
One way to prevent such a number from wrongfully being declared probably prime is to combine a strong probable prime test with a Lucas probable prime test, as in the Baillie–PSW primality test.
There are infinitely many strong pseudoprimes to any base.[2]
Examples
The first strong pseudoprimes to base 2 are
2047, 3277, 4033, 4681, 8321, 15841, 29341, 42799, 49141, 52633, 65281, 74665, 80581, 85489, 88357, 90751, ... {{OEIS|id=A001262}}.
The first to base 3 are
121, 703, 1891, 3281, 8401, 8911, 10585, 12403, 16531, 18721, 19345, 23521, 31621, 44287, 47197, 55969, 63139, 74593, 79003, 82513, 87913, 88573, 97567, ... {{OEIS|id=A020229}}.
The first to base 5 are
781, 1541, 5461, 5611, 7813, 13021, 14981, 15751, 24211, 25351, 29539, 38081, 40501, 44801, 53971, 79381, ... {{OEIS|id=A020231}}.
For base 4, see {{oeis|id=A020230}}, and for base 6 to 100, see {{oeis|id=A020232}} to {{oeis|id=A020326}}.
By testing the above conditions to several bases, one gets somewhat more powerful primality tests than by using one base alone.
For example, there are only 13 numbers less than 25·109 that are strong pseudoprimes to bases 2, 3, and 5 simultaneously.
They are listed in Table 7 of.[2] The smallest such number is 25326001.
This means that, if n is less than 25326001 and n is a strong probable prime to bases 2, 3, and 5, then n is prime.
Carrying this further, 3825123056546413051 is the smallest number that is a strong pseudoprime to the 9 bases 2, 3, 5, 7, 11, 13, 17, 19, and 23.[6]
[7]So, if n is less than 3825123056546413051 and n is a strong probable prime to these 9 bases, then n is prime.
By judicious choice of bases that are not necessarily prime, even better tests can be constructed. For example, there is no composite  that is a strong pseudoprime to all of the seven bases 2, 325, 9375, 28178, 450775, 9780504, and 1795265022.[8]
that is a strong pseudoprime to all of the seven bases 2, 325, 9375, 28178, 450775, 9780504, and 1795265022.[8]
Smallest strong pseudoprime to base n
| n | Least SPSP | n | Least SPSP | n | Least SPSP | n | Least SPSP |
| 1 | 9 | 33 | 545 | 65 | 33 | 97 | 49 |
| 2 | 2047 | 34 | 33 | 66 | 65 | 98 | 9 |
| 3 | 121 | 35 | 9 | 67 | 33 | 99 | 25 |
| 4 | 341 | 36 | 35 | 68 | 25 | 100 | 9 |
| 5 | 781 | 37 | 9 | 69 | 35 | 101 | 25 |
| 6 | 217 | 38 | 39 | 70 | 69 | 102 | 133 |
| 7 | 25 | 39 | 133 | 71 | 9 | 103 | 51 |
| 8 | 9 | 40 | 39 | 72 | 85 | 104 | 15 |
| 9 | 91 | 41 | 21 | 73 | 9 | 105 | 451 |
| 10 | 9 | 42 | 451 | 74 | 15 | 106 | 15 |
| 11 | 133 | 43 | 21 | 75 | 91 | 107 | 9 |
| 12 | 91 | 44 | 9 | 76 | 15 | 108 | 91 |
| 13 | 85 | 45 | 481 | 77 | 39 | 109 | 9 |
| 14 | 15 | 46 | 9 | 78 | 77 | 110 | 111 |
| 15 | 1687 | 47 | 65 | 79 | 39 | 111 | 55 |
| 16 | 15 | 48 | 49 | 80 | 9 | 112 | 65 |
| 17 | 9 | 49 | 25 | 81 | 91 | 113 | 57 |
| 18 | 25 | 50 | 49 | 82 | 9 | 114 | 115 |
| 19 | 9 | 51 | 25 | 83 | 21 | 115 | 57 |
| 20 | 21 | 52 | 51 | 84 | 85 | 116 | 9 |
| 21 | 221 | 53 | 9 | 85 | 21 | 117 | 49 |
| 22 | 21 | 54 | 55 | 86 | 85 | 118 | 9 |
| 23 | 169 | 55 | 9 | 87 | 247 | 119 | 15 |
| 24 | 25 | 56 | 55 | 88 | 87 | 120 | 91 |
| 25 | 217 | 57 | 25 | 89 | 9 | 121 | 15 |
| 26 | 9 | 58 | 57 | 90 | 91 | 122 | 65 |
| 27 | 121 | 59 | 15 | 91 | 9 | 123 | 85 |
| 28 | 9 | 60 | 481 | 92 | 91 | 124 | 25 |
| 29 | 15 | 61 | 15 | 93 | 25 | 125 | 9 |
| 30 | 49 | 62 | 9 | 94 | 93 | 126 | 25 |
| 31 | 15 | 63 | 529 | 95 | 1891 | 127 | 9 |
| 32 | 25 | 64 | 9 | 96 | 95 | 128 | 49 |
References
2. ^1 2 {{cite journal|author1=Carl Pomerance|authorlink1=Carl Pomerance|author2=John L. Selfridge|authorlink2=John L. Selfridge|author3=Samuel S. Wagstaff, Jr.|authorlink3=Samuel S. Wagstaff, Jr.|title=The pseudoprimes to 25·109|journal=Mathematics of Computation|date=July 1980|volume=35|issue=151|pages=1003–1026|url=http://www.math.dartmouth.edu/~carlp/PDF/paper25.pdf| doi=10.1090/S0025-5718-1980-0572872-7 }}
3. ^{{cite journal |title=Evaluation and Comparison of Two Efficient Probabilistic Primality Testing Algorithms |author=Louis Monier |journal=Theoretical Computer Science |date=1980 |volume=12 |pages=97–108 |doi=10.1016/0304-3975(80)90007-9}}
4. ^Rabin, Probabilistic Algorithm for Testing Primality. Journal of Number Theory, 12 pp. 128-138, 1980.
5. ^{{cite journal|title=Constructing Carmichael Numbers Which Are Strong Pseudoprimes to Several Bases|journal=Journal of Symbolic Computation|date=August 1995|volume=20|issue=2|pages=151–161|author=F. Arnault|url=http://www.sciencedirect.com/science/article/pii/S0747717185710425|doi=10.1006/jsco.1995.1042}}
6. ^{{cite journal|title=Finding Strong Pseudoprimes to Several Bases. II|journal=Mathematics of Computation|year=2003|volume=72|issue=244|pages=2085–2097|author1=Zhenxiang Zhang|author2=Min Tang|doi=10.1090/S0025-5718-03-01545-X }}
7. ^{{cite arXiv |last1=Jiang |first1=Yupeng |last2=Deng |first2=Yingpu |eprint=1207.0063v1|title=Strong pseudoprimes to the first 9 prime bases |class=math.NT |year=2012 |version= }}
8. ^{{cite web | url=https://miller-rabin.appspot.com | title=SPRP Records | access-date=3 June 2015}}
- Ben Chipman
- Ben Chiu
- Bench Jeweler
- Bench Lake (Glacier County, Montana)
- Benchland
- Bench lathe
- Bench (law)
- Benchley
- Benchmark Asset Management Company Private Ltd
- Benchmark (disambiguation)
- Benchmark-driven investment strategy
- Benchmark Electronics
- Benchmark Electronics, Inc.
- Bench mark program
- Benchmark program
- Benchmark Recordings
- Benchmark, South Dakota
- Benchmark test
- Bench memo
- Bench memorandum
- Bench mounting
- Bencho
- Bench of counts of westphalia
- Bench of Counts of Westphalia
- Ben Choud