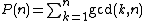- References
In number theory, the gcd-sum function,[1]
also called Pillai's arithmetical function,[1] is defined for every  by
by
or equivalently[1]
where  is a divisor of
is a divisor of  and
and  is Euler's totient function.
is Euler's totient function.
it also can be written as[2]
where,  is the Divisor function, and
is the Divisor function, and  is the Möbius function.
is the Möbius function.
This multiplicative arithmetical function was introduced by the Indian mathematician Subbayya Sivasankaranarayana Pillai in 1933.[3]
[4]References
1. ^1 2 {{cite journal |author=Lászlo Tóth |title=A survey of gcd-sum functions |journal=J. Integer Sequences |volume=13 |year=2010}}
2. ^http://math.stackexchange.com/questions/135351/sum-of-gcdk-n
3. ^{{cite journal |author=S. S. Pillai |title=On an arithmetic function |journal=Annamalai University Journal |volume=II |year=1933 |pages=242–248}}
4. ^{{cite journal |last1=Broughan |first1=Kevin |title=The gcd-sum function |journal=Journal of Integer Sequences |date=2002 |volume=4 |issue=Article 01.2.2 |pages=1-19 }}
{{oeis|A018804}}2. ^http://math.stackexchange.com/questions/135351/sum-of-gcdk-n
3. ^{{cite journal |author=S. S. Pillai |title=On an arithmetic function |journal=Annamalai University Journal |volume=II |year=1933 |pages=242–248}}
4. ^{{cite journal |last1=Broughan |first1=Kevin |title=The gcd-sum function |journal=Journal of Integer Sequences |date=2002 |volume=4 |issue=Article 01.2.2 |pages=1-19 }}
1 : Arithmetic functions
- Holocheila
- Holocheila longipedunculata
- Holochila absimilis
- Holochila agatha
- Holochila androdus
- Holochila anita
- Holochila ardosiacea
- Holochila biaka
- Holochila bimaculosa
- Holochila butleri
- Holochila fulgens
- Holochila gilberti
- Holochila harterti
- Holochila helenita
- Holochila hyacinthina
- Holochila intensa
- Holochila lamia
- Holochila limbata
- Holochila margarita
- Holochila marginata
- Holochila meforensis
- Holochila neurapacuna
- Holochila persimilis
- Holochila purpurea
- Holochila regina