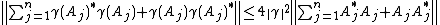“Pisier–Ringrose inequality”的意思、由来-开放百科全书

词条

Pisier–Ringrose inequality

释义

Statement
See also
Notes
References

In mathematics, Pisier–Ringrose inequality is an inequality in the theory of C*-algebras which was proved by Gilles Pisier in 1978 affirming a conjecture of John Ringrose. It is an extension of the Grothendieck inequality.

Statement

Theorem.^[1]^[2] If is a bounded, linear mapping of one C*-algebra into another C*-algebra , then

for each finite set 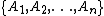of elements of .

Notes

1. ^{{harvtxt|Kadison|1993}}, Theorem D, p. 60.
2. ^{{harvtxt|Pisier|1978}}, Corollary 2.3, p. 410.

References

{{citation

| last = Pisier | first = Gilles | authorlink = Gilles Pisier
| doi = 10.1016/0022-1236(78)90038-1
| issue = 3
| journal = Journal of Functional Analysis
| mr = 512252
| pages = 397–415
| title = Grothendieck's theorem for noncommutative C^∗-algebras, with an appendix on Grothendieck's constants
| volume = 29
| year = 1978}}.

{{citation

| last = Kadison | first = Richard V. | authorlink = Richard Kadison
| issue = 1
| journal = Journal of Operator Theory
| mr = 1277964
| pages = 57–67
| title = On an inequality of Haagerup–Pisier
| url = http://www.theta.ro/jot/archive/1993-029-001/1993-029-001-004.html
| volume = 29
| year = 1993}}.{{DEFAULTSORT:Pisier-Ringrose inequality}}

2 : Inequalities|Operator algebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Statement

See also

Notes

References