1. Examples

2. Properties

3. Operators

4. References

A sublinear function (or functional, as is more often used in functional analysis), in linear algebra and related areas of mathematics, is a function 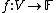on a vector space V over 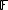an ordered field (e.g. the real numbers 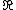), which satisfies

for any positive and any (positive homogeneity), and

for any x, y ∈ V (subadditivity).

In functional analysis the name Banach functional is used for sublinear function, especially when formulating Hahn–Banach theorem.

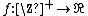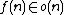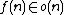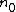In computer science, a function is called sublinear if in asymptotic notation (notice the small ). Formally, if and only if, for any given , there exists an such that^[1]

This means that for any linear function 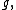for sufficiently large input grows slower than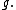

Examples

• Every (semi-)norm is a sublinear function. The opposite is not true, because (semi-)norms can have their domain vector space over any field (not necessarily ordered) and must have 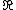as their codomain.

Properties

• Every sublinear function is a convex functional.

Operators

The concept can be extended to operators that are homogeneous and subadditive. This requires only that the codomain be, say, an ordered vector space to make sense of the conditions.

References

• The brilliant green complete singles collection '97-'08
• The Brilliant Green:Complete Singles Collection '97-'08
• The Brilliant Inventions
• The Brilliant Mistakes
• The Brilly-Allent Tour
• The Brimnes
• The Bringer of Jollity
• The Bringer of Old Age
• The Bringer of War
• The Bringers of Wonder, Part One
• The Bringers of Wonder, Part Two
• The brink
• The Brinkerhoff
• The Brink of the Ex-Stink-Tion
• The Brinks Job
• The Brink (TV series)
• The Briones Brothers
• The Brisbane River
• The Brisbane Times
• The Brisbane Worker
• The Brisons
• The Bristol Boxkite
• The Bristol Classic Boat Company
• The Bristolian
• The Bristol International Balloon Fiesta