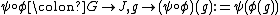- Transitive relation
- See also
- References
In the mathematical fields of category theory and abstract algebra, a subquotient is a quotient object of a subobject. Subquotients are particularly important in abelian categories, and in group theory, where they are also known as sections, though this conflicts with a different meaning in category theory.
For example, of the 26 sporadic groups, 20 are subquotients of the monster group, and are referred to as the "Happy Family", while the other 6 are pariah groups.
A quotient of a subrepresentation of a representation (of, say, a group) might be called a subquotient representation; e.g., Harish-Chandra's subquotient theorem.[1]
In constructive set theory, where the law of excluded middle does not necessarily hold, one can consider the relation 'subquotient of' as replacing the usual order relation(s) on cardinals. When one has the law of the excluded middle, then a subquotient 
of 
is either the empty set or there is an onto function 
. This order relation is traditionally denoted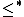 
. If additionally the axiom of choice holds, then has a one-to-one function to and this order relation is the usual 
on corresponding cardinals.
Transitive relation
The relation »is subquotient of« is transitive.
- Proof
Let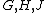 
groups 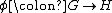and 
and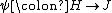 
be group homomorphisms, then also the composition
is a homomorphism.
If 
is a subgroup of 
and 
a subgroup of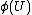 
, then 
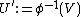is a subgroup of 
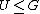. We have 
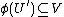, indeed 
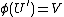, because every 
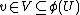has a preimage in . Thus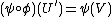 
. This means that the image, say 
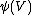, of a subgroup, say , of 
is also the image of a subgroup, namely 
under 
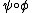, of .
In other words: If 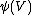is a subquotient of 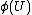and 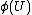is subquotient of then 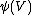is subquotient of . ■
See also
- Homological algebra
References
- Arbutus floribunda
- Arbutus idaea
- Arbutus integrifolia
- Arbutus intermedia
- Arbutus Lake (Grand Traverse County, Michigan)
- Arbutus Lake (Michigan)
- Arbutus laurifolia
- Arbutus laurina
- Arbutus longifolia
- Arbutus lucida
- Arbutus macrophylla
- Arbutus madrensis
- Arbutus microphylla
- Arbutus mollis
- Arbutus nothocomaros
- Arbutus Oak
- Arbutus occidentalis
- Arbutus paniculata
- Arbutus peninsularis
- Arbutus petiolaris
- Arbutus procera
- Arbutus procumbens
- Arbutus prunifolia
- Arbutus Ridge Seaside Community for Active Adults
- Arbutus rubescens