“Summation by parts”的意思、由来-开放百科全书

词条

Summation by parts

释义

Statement
Newton series
Method
Similarity with an integration by parts
Applications
See also
References

{{Redirect|Abel transformation|another transformation|Abel transform}}

In mathematics, summation by parts transforms the summation of products of sequences into other summations, often simplifying the computation or (especially) estimation of certain types of sums. The summation by parts formula is sometimes called Abel's lemma or Abel transformation.

Statement

Suppose and are two sequences. Then,

Using the forward difference operator , it can be stated more succinctly as

Note that summation by parts is an analogue to integration by parts:

An alternative statement is

which is analogous to the integration by parts formula for semimartingales.

Note also that although applications almost always deal with convergence of sequences, the statement is purely algebraic and will work in any field. It will also work when one sequence is in a vector space, and the other is in the relevant field of scalars.

Newton series

The formula is sometimes given in one of these - slightly different - forms

which represent a special case () of the more general rule

both result from iterated application of the initial formula. The auxiliary quantities are Newton series:

and

A remarkable, particular () result is the noteworthy identity

Here, is the binomial coefficient.

Method

For two given sequences and , with , one wants to study the sum of the following series:

If we define

then for every 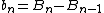and

Finally

This process, called an Abel transformation, can be used to prove several criteria of convergence for .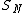

Similarity with an integration by parts

The formula for an integration by parts is

Beside the boundary conditions, we notice that the first integral contains two multiplied functions, one which is integrated in the final integral ( becomes ) and one which is differentiated ( becomes ).

The process of the Abel transformation is similar, since one of the two initial sequences is summed ( becomes ) and the other one is differenced ( becomes ).

Applications

It is used to prove Kronecker's lemma, which in turn, is used to prove a version of the strong law of large numbers under variance constraints.
Summation by parts is frequently used to prove Abel's theorem and Dirichlet's test.
One can also use this technique to prove Abel's test: If is a convergent series, and a bounded monotone sequence, then converges.

Summation by parts gives

where a is the limit of . As is convergent, is bounded independently of , say by . As go to zero, so go the first two terms. The third term goes to zero by the Cauchy criterion for . The remaining sum is bounded by

by the monotonicity of , and also goes to zero as .

Using the same proof as above, one can show that if
1. the partial sums form a bounded sequence independently of ;
2. (so that the sum goes to zero as goes to infinity)

then converges.

In both cases, the sum of the series satisfies:

References

{{planetmathref|id=3843|title=Abel's lemma}}

3 : Summability methods|Real analysis|Lemmas

随便看