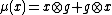“Primitive element (co-algebra)”的意思、由来-开放百科全书

词条

Primitive element (co-algebra)

释义

References

In algebra, a primitive element of a co-algebra C (over an element g) is an element x that satisfies

where is the co-multiplication and g is an element of C that maps to the multiplicative identity 1 of the base field under the co-unit (g is called group-like).

If C is a bi-algebra, i.e., a co-algebra that is also an algebra (with certain compatibility conditions satisfied), then one usually takes g to be 1, the multiplicative identity of C. The bi-algebra C is said to be primitively generated if it is generated by primitive elements (as an algebra).

If C is a bi-algebra, then the set of primitive elements form a Lie algebra with the usual commutator bracket 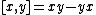(graded commutator if C is graded).

If A is a connected graded cocommutative Hopf algebra over a field of characteristic zero, then the Milnor–Moore theorem states the universal enveloping algebra of the graded Lie algebra of primitive elements of A is isomorphic to A. (This also holds under slightly weaker requirements.)

References

http://www.encyclopediaofmath.org/index.php/Primitive_element_in_a_co-algebra

1 : Coalgebras

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。