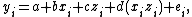“Principle of marginality”的意思、由来-开放百科全书

In statistics, the principle of marginality is the fact that the average (or main) effects, of variables in an analysis are marginal to their interaction effect—that is, the main effect of one explanatory variable captures the effect of that variable averaged over all values of a second explanatory variable whose value influences the first variable's effect. The principle of marginality implies that, in general, it is wrong to test, estimate, or interpret main effects of explanatory variables where the variables interact or, similarly, to model interaction effects but delete main effects that are marginal to

them.^[1] While such models are interpretable, they lack applicability, as they ignore the dependence of a variable's effect upon another variable's value.

Nelder^[2] and Venables^[3] have argued strongly for the importance of this principle in regression analysis.

Regression form

If two independent continuous variables, say x and z, both influence a dependent variable y, and if the extent of the effect of each independent variable depends on the level of the other independent variable then the regression equation can be written as:

where i indexes observations, a is the intercept term, b, c, and d are effect size parameters to be estimated, and e is the error term.

If this is the correct model, then the omission of any of the right-side terms would be incorrect, resulting in misleading interpretation of the regression results.

With this model, the effect of x upon y is given by the partial derivative of y with respect to x; this is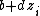

, which depends on the specific value

at which the partial derivative is being evaluated. Hence, the main effect of x – the effect averaged over all values of z – is meaningless as it depends on the design of the experiment (specifically on the relative frequencies of the various values of z) and not just on the underlying relationships. Hence:

See also

References

1. ^Fox, J. Regression Notes.
2. ^{{Cite journal | last1 = Nelder | first1 = J. A. |authorlink = John Nelder| title = A Reformulation of Linear Models | journal = Journal of the Royal Statistical Society | volume = 140 | issue = 1 | pages = 48–77 | doi = 10.2307/2344517 | year = 1977 | pmid = | pmc = }} (Section 2.1: The Neglect of Marginality)
3. ^Venables, W.N. (1998). "Exegeses on Linear Models". Paper presented to the S-PLUS User’s Conference Washington, DC, 8–9 October 1998.
4. ^See Venables, p.13: "... testing main effects in the presence of an interaction is a violation of the marginality principle".
5. ^See Venables, p.14/15, about the S-Plus command drop1, which does not drop the main effect terms from a model with interaction: "To my delight I see that marginality constraints between factor terms are by default honoured". In R, the marginality requirement of the dropterm function (in package MASS) is stated in the Reference Manual.
6. ^The above regression model, with two independent continuous variables, is presented with a numerical example, in Stata, as Case 3 in What happens if you omit the main effect in a regression model with an interaction?.

Regression form

See also

References

External links