“Super-Poulet number”的意思、由来-开放百科全书

词条

Super-Poulet number

释义

Super-Poulet numbers with 3 or more distinct prime divisors
External links

A super-Poulet number is a Poulet number, or pseudoprime to base 2, whose every divisor d divides

2^d − 2.

For example, 341 is a super-Poulet number: it has positive divisors {1, 11, 31, 341} and we have:

(2¹¹ - 2) / 11 = 2046 / 11 = 186

(2³¹ - 2) / 31 = 2147483646 / 31 = 69273666

(2³⁴¹ - 2) / 341 = 13136332798696798888899954724741608669335164206654835981818117894215788100763407304286671514789484550

When 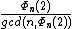is not prime, then it and every divisor of it are a pseudoprime to base 2, and a super-Poulet number.

The super-Poulet numbers below 10,000 are {{OEIS|id=A050217}}:

n
1	341 = 11 × 31
2	1387 = 19 × 73
3	2047 = 23 × 89
4	2701 = 37 × 73
5	3277 = 29 × 113
6	4033 = 37 × 109
7	4369 = 17 × 257
8	4681 = 31 × 151
9	5461 = 43 × 127
10	7957 = 73 × 109
11	8321 = 53 × 157

Super-Poulet numbers with 3 or more distinct prime divisors

It is relatively easy to get super-Poulet numbers with 3 distinct prime divisors. If you find three Poulet numbers with three common prime factors, you get a super-Poulet number, as you built the product of the three prime factors.

Example:

2701 = 37 * 73 is a Poulet number,

4033 = 37 * 109 is a Poulet number,

7957 = 73 * 109 is a Poulet number;

so 294409 = 37 * 73 * 109 is a Poulet number too.

Super-Poulet numbers with up to 7 distinct prime factors you can get with the following numbers:

{ 103, 307, 2143, 2857, 6529, 11119, 131071 }
{ 709, 2833, 3541, 12037, 31153, 174877, 184081 }
{ 1861, 5581, 11161, 26041, 37201, 87421, 102301 }
{ 6421, 12841, 51361, 57781, 115561, 192601, 205441 }

For example, 1118863200025063181061994266818401 = 6421 * 12841 * 51361 * 57781 * 115561 * 192601 * 205441 is a super-Poulet number with 7 distinct prime factors and 120 Poulet numbers.

External links

{{mathworld|Super-PouletNumber}}
Numericana

1 : Integer sequences

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。