“Superstrong cardinal”的意思、由来-开放百科全书

词条

Superstrong cardinal

释义

References

In mathematics, a cardinal number κ is called superstrong if and only if there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point κ and 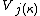⊆ M.

Similarly, a cardinal κ is n-superstrong if and only if there exists an elementary embedding j : V → M from V into a transitive inner model M with critical point κ and 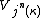⊆ M. Akihiro Kanamori has shown that the consistency strength of an n+1-superstrong cardinal exceeds that of an n-huge cardinal for each n > 0.

References

{{cite book|last=Kanamori|first=Akihiro|authorlink=Akihiro Kanamori|year=2003|publisher=Springer|title=The Higher Infinite : Large Cardinals in Set Theory from Their Beginnings|edition=2nd|isbn=3-540-00384-3}}

2 : Set theory|Large cardinals

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。