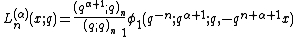“Q-Laguerre polynomials”的意思、由来-开放百科全书

词条

Q-Laguerre polynomials

释义

Definition
Orthogonality
Recurrence and difference relations
Rodrigues formula
Generating function
Relation to other polynomials
References

{{DISPLAYTITLE: q-Laguerre polynomials}}{{see also|big q-Laguerre polynomials|continuous q-Laguerre polynomials|little q-Laguerre polynomials}}

In mathematics, the q-Laguerre polynomials, or generalized Stieltjes–Wigert polynomials P{{su|b=n|p=(α)}}(x;q) are a family of basic hypergeometric orthogonal polynomials in the basic Askey scheme introduced by {{harvs|txt | last=Moak|first=Daniel S.|title=The q-analogue of the Laguerre polynomials|journal=. J. Math. Anal. Appl.| volume=81|issue=1|pages=20–47|year=1981}}. {{harvs|txt | last1=Koekoek | first1=Roelof | last2=Lesky | first2=Peter A. | last3=Swarttouw | first3=René F. | title=Hypergeometric orthogonal polynomials and their q-analogues | publisher=Springer-Verlag | location=Berlin, New York | series=Springer Monographs in Mathematics | isbn=978-3-642-05013-8 | doi=10.1007/978-3-642-05014-5 | mr=2656096 | year=2010|loc=14}} give a detailed list of their properties.

Definition

The q-Laguerre polynomials are given in terms of basic hypergeometric functions and the Pochhammer symbol by

Orthogonality

Recurrence and difference relations

Rodrigues formula

Generating function

Relation to other polynomials

References

{{Citation | last1=Gasper | first1=George | last2=Rahman | first2=Mizan | title=Basic hypergeometric series | publisher=Cambridge University Press | edition=2nd | series=Encyclopedia of Mathematics and its Applications | isbn=978-0-521-83357-8 | doi=10.2277/0521833574 | mr=2128719 | year=2004 | volume=96}}
{{Citation | last1=Koekoek | first1=Roelof | last2=Lesky | first2=Peter A. | last3=Swarttouw | first3=René F. | title=Hypergeometric orthogonal polynomials and their q-analogues | publisher=Springer-Verlag | location=Berlin, New York | series=Springer Monographs in Mathematics | isbn=978-3-642-05013-8 | doi=10.1007/978-3-642-05014-5 | mr=2656096 | year=2010}}
{{dlmf|id=18|title=|first=Tom H. |last=Koornwinder|first2=Roderick S. C.|last2= Wong|first3=Roelof |last3=Koekoek||first4=René F. |last4=Swarttouw}}
{{citation | last=Moak|first=Daniel S.|title=The q-analogue of the Laguerre polynomials|journal=J. Math. Anal. Appl.| volume=81|issue=1|pages=20–47|year=1981| doi=10.1016/0022-247X(81)90048-2 |mr=618759}}

3 : Orthogonal polynomials|Q-analogs|Special hypergeometric functions

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。