“Quantum machine learning”的意思、由来-开放百科全书

Quantum-enhanced machine learning refers to quantum algorithms that solve tasks in machine learning, thereby improving and often expediting classical machine learning techniques. Such algorithms typically require one to encode the given classical data set into a quantum computer to make it accessible for quantum information processing. Subsequently, quantum information processing routines are applied and the result of the quantum computation is read out by measuring the quantum system. For example, the outcome of the measurement of a qubit reveals the result of a binary classification task. While many proposals of quantum machine learning algorithms are still purely theoretical and require a full-scale universal quantum computer to be tested, others have been implemented on small-scale or special purpose quantum devices.

Linear algebra simulation with quantum amplitudes

A number of quantum algorithms for machine learning are based on the idea of amplitude encoding, that is, to associate the amplitudes of a quantum state with the inputs and outputs of computations.^[27]^[28]^[29]^[30] Since a state of

qubits is described by

complex amplitudes, this information encoding can allow for an exponentially compact representation. Intuitively, this corresponds to associating a discrete probability distribution over binary random variables with a classical vector. The goal of algorithms based on amplitude encoding is to formulate quantum algorithms whose resources grow polynomially in the number of qubits

, which amounts to a logarithmic growth in the number of amplitudes and thereby the dimension of the input.

Many quantum machine learning algorithms in this category are based on variations of the quantum algorithm for linear systems of equations^[31] (colloquially called HHL, after the paper's authors) which, under specific conditions, performs a matrix inversion using an amount of physical resources growing only logarithmically in the dimensions of the matrix. One of these conditions is that a Hamiltonian which entrywise corresponds to the matrix can be simulated efficiently, which is known to be possible if the matrix is sparse^[32] or low rank.^[33] For reference, any known classical algorithm for matrix inversion requires a number of operations that grows at least quadratically in the dimension of the matrix.

Quantum matrix inversion can be applied to machine learning methods in which the training reduces to solving a linear system of equations, for example in least-squares linear regression,^[28]^[29] the least-squares version of support vector machines,^[27] and Gaussian processes.^[30]

A crucial bottleneck of methods that simulate linear algebra computations with the amplitudes of quantum states is state preparation, which often requires one to initialise a quantum system in a state whose amplitudes reflect the features of the entire dataset. Although efficient methods for state preparation are known for specific cases,^[34]^[35] this step easily hides the complexity of the task.^[36]^[37]

Quantum machine learning algorithms based on Grover search

Another approach to improving classical machine learning with quantum information processing uses amplitude amplification methods based on Grover's search algorithm, which has been shown to solve unstructured search problems with a quadratic speedup compared to classical algorithms. These quantum routines can be employed for learning algorithms that translate into an unstructured search task, as can be done, for instance, in the case of the k-medians^[38] and the k-nearest neighbors algorithms.^[7] Another application is a quadratic speedup in the training of perceptron.^[39]

Amplitude amplification is often combined with quantum walks to achieve the same quadratic speedup. Quantum walks have been proposed to enhance Google's PageRank algorithm^[40] as well as the performance of reinforcement learning agents in the projective simulation framework.^[41]

Quantum-enhanced reinforcement learning

Reinforcement learning is a branch of machine learning distinct from supervised and unsupervised learning, which also admits quantum enhancements.^[42]^[41]^[43]^[44] In quantum-enhanced reinforcement learning, a quantum agent interacts with a classical environment and occasionally receives rewards for its actions, which allows the agent to adapt its behavior—in other words, to learn what to do in order to gain more rewards. In some situations, either because of the quantum processing capability of the agent,^[41] or due to the possibility to probe the environment in superpositions,^[26] a quantum speedup may be achieved. Implementations of these kinds of protocols in superconducting circuits^[45] and in systems of trapped ions^[46]^[47] have been proposed.

Quantum annealing

Quantum annealing is an optimization technique used to determine the local minima and maxima of a function over a given set of candidate functions. This is a method of discretizing a function with many local minima or maxima in order to determine the observables of the function. The process can be distinguished from Simulated annealing by the Quantum tunneling process, by which particles tunnel through kinetic or potential barriers from a high state to a low state. Quantum annealing starts from a superposition of all possible states of a system, weighted equally. Then the time-dependent Schrödinger equation guides the time evolution of the system, serving to affect the amplitude of each state as time increases. Eventually, the ground state can be reached to yield the instantaneous Hamiltonian of the system.

Quantum sampling techniques

Sampling from high-dimensional probability distributions is at the core of a wide spectrum of computational techniques with important applications across science, engineering, and society. Examples include deep learning, probabilistic programming, and other machine learning and artificial intelligence applications.

A computationally hard problem, which is key for some relevant machine learning tasks, is the estimation of averages over probabilistic models defined in terms of a Boltzmann distribution. Sampling from generic probabilistic models is hard: algorithms relying heavily on sampling are expected to remain intractable no matter how large and powerful classical computing resources become. Even though quantum annealers, like those produced by D-Wave Systems, were designed for challenging combinatorial optimization problems, it has been recently recognized as a potential candidate to speed up computations that rely on sampling by exploiting quantum effects.^[48]

Some research groups have recently explored the use of quantum annealing hardware for training Boltzmann machines and deep neural networks.^[49]^[50]^[51]^[52] The standard approach to training Boltzmann machines relies on the computation of certain averages that can be estimated by standard sampling techniques, such as Markov chain Monte Carlo algorithms. Another possibility is to rely on a physical process, like quantum annealing, that naturally generates samples from a Boltzmann distribution. The objective is to find the optimal control parameters that best represent the empirical distribution of a given dataset.

The D-Wave 2X system hosted at NASA Ames Research Center has been recently used for the learning of a special class of restricted Boltzmann machines that can serve as a building block for deep learning architectures.^[51] Complementary work that appeared roughly simultaneously showed that quantum annealing can be used for supervised learning in classification tasks.^[49] The same device was later used to train a fully connected Boltzmann machine to generate, reconstruct, and classify down-scaled, low-resolution handwritten digits, among other synthetic datasets.^[50] In both cases, the models trained by quantum annealing had a similar or better performance in terms of quality. The ultimate question that drives this endeavour is whether there is quantum speedup in sampling applications. Experience with the use of quantum annealers for combinatorial optimization suggests the answer is not straightforward.

Inspired by the success of Boltzmann machines based on classical Boltzmann distribution, a new machine learning approach based on quantum Boltzmann distribution of a transverse-field Ising Hamiltonian was recently proposed.^[53] Due to the non-commutative nature of quantum mechanics, the training process of the quantum Boltzmann machine can become nontrivial. This problem was, to some extent, circumvented by introducing bounds on the quantum probabilities, allowing the authors to train the model efficiently by sampling. It is possible that a specific type of quantum Boltzmann machine has been trained in the D-Wave 2X by using a learning rule analogous to that of classical Boltzmann machines.^[50]^[52]^[54]

Quantum annealing is not the only technology for sampling. In a prepare-and-measure scenario, a universal quantum computer prepares a thermal state, which is then sampled by measurements. This can reduce the time required to train a deep restricted Boltzmann machine, and provide a richer and more comprehensive framework for deep learning than classical computing.^[55] The same quantum methods also permit efficient training of full Boltzmann machines and multi-layer, fully connected models and do not have well-known classical counterparts. Relying on an efficient thermal state preparation protocol starting from an arbitrary state, quantum-enhanced Markov logic networks exploit the symmetries and the locality structure of the probabilistic graphical model generated by a first-order logic template.^[56] This provides an exponential reduction in computational complexity in probabilistic inference, and, while the protocol relies on a universal quantum computer, under mild assumptions it can be embedded on contemporary quantum annealing hardware.

Quantum neural networks

Quantum analogues or generalizations of classical neural nets are often referred to as quantum neural networks. The term is claimed by a wide range of approaches, including the implementation and extension of neural networks using photons, layered variational circuits or quantum Ising-type models. Quantum neural networks are often defined as an expansion on Deutsch's model of a quantum computational network.^[57] Within this model, nonlinear and irreversible gates, dissimilar to the Hamiltonian operator, are deployed to speculate the given data set.^[57] Such gates make certain phases unable to be observed and generate specific oscillations.^[57] Quantum neural networks apply the principals quantum information and quantum computation to classical neurocomputing.^[58] Current research shows that QNN can exponentially increase the amount of computing power and the degrees of freedom for a computer, which is limited for a classical computer to its size.^[58] A quantum neural network has computational capabilities to decrease the number of steps, qubits used, and computation time.^[57] The wave function to quantum mechanics is the neuron for Neural networks. To test quantum applications in a neural network, quantum dot molecules are deposited on a substrate of GaAs or similar to record how they communicate with one another. Each quantum dot can be referred as an island of electric activity, and when such dots are close enough (approximately 10±20 nm)^[59] electrons can tunnel underneath the islands. An even distribution across the substrate in sets of two create dipoles and ultimately two spin states, up or down. These states are commonly known as qubits with corresponding states of |0> and |1> in Dirac notation.^[59]

Hidden Quantum Markov Models

Hidden Quantum Markov Models^[60] (HQMMs) are a quantum-enhanced version of classical Hidden Markov Models (HMMs), which are typically used to model sequential data in various fields like robotics and natural language processing. Unlike the approach taken by other quantum-enhanced machine learning algorithms, HQMMs can be viewed as models inspired by quantum mechanics that can be run on classical computers as well.^[61] Where classical HMMs use probability vectors to represent hidden 'belief' states, HQMMs use the quantum analogue: density matrices. Recent work has shown that these models can be successfully learned by maximizing the log-likelihood of the given data via classical optimization, and there is some empirical evidence that these models can better model sequential data compared to classical HMMs in practice, although further work is needed to determine exactly when and how these benefits are derived.^[61] Additionally, since classical HMMs are a particular kind of Bayes net, an exciting aspect of HQMMs is that the techniques used show how we can perform quantum-analogous Bayesian inference, which should allow for the general construction of the quantum versions of probabilistic graphical models.^[61]

Fully quantum machine learning

In the most general case of quantum machine learning, both the learning device and the system under study, as well as their interaction, are fully quantum. This section gives a few examples of results on this topic.

One class of problem that can benefit from the fully quantum approach is that of 'learning' unknown quantum states, processes or measurements, in the sense that one can subsequently reproduce them on another quantum system. For example, one may wish to learn a measurement that discriminates between two coherent states, given not a classical description of the states to be discriminated, but instead a set of example quantum systems prepared in these states. The naive approach would be to first extract a classical description of the states and then implement an ideal discriminating measurement based on this information. This would only require classical learning. However, one can show that a fully quantum approach is strictly superior in this case.^[62] (This also relates to work on quantum pattern matching.^[63]) The problem of learning unitary transformations can be approached in a similar way.^[64]

Going beyond the specific problem of learning states and transformations, the task of clustering also admits a fully quantum version, wherein both the oracle which returns the distance between data-points and the information processing device which runs the algorithm are quantum.^[65] Finally, a general framework spanning supervised, unsupervised and reinforcement learning in the fully quantum setting was introduced in,^[26] where it was also shown that the possibility of probing the environment in superpositions permits a quantum speedup in reinforcement learning.

Classical learning applied to quantum problems

The term quantum machine learning is also used for approaches that apply classical methods of machine learning to the study of quantum systems. A prime example is the use of classical learning techniques to process large amounts of experimental or calculated (for example by solving Schrodinger's equation data in order to characterize an unknown quantum system (for instance in the context of quantum information theory and for the development of quantum technologies or computational materials design), but there are also more exotic applications.

Noisy data

The ability to experimentally control and prepare increasingly complex quantum systems brings with it a growing need to turn large and noisy data sets into meaningful information. This is a problem that has already been studied extensively in the classical setting, and consequently, many existing machine learning techniques can be naturally adapted to more efficiently address experimentally relevant problems. For example, Bayesian methods and concepts of algorithmic learning can be fruitfully applied to tackle quantum state classification,^[66] Hamiltonian learning,^[67] and the characterization of an unknown unitary transformation.^[68]^[69] Other problems that have been addressed with this approach are given in the following list:

Calculated and noise-free data

Quantum machine learning can also be applied to dramatically accelerate the prediction of quantum properties of molecules and materials.^[79] This can be helpful for the computational design of new molecules or materials. Some examples include

Variational Circuits

Variational circuits are a family of algorithms which utilize training based on circuit parameters and an objective function.^[86] Variational circuits are generally composed of a classical device communicating input parameters (random or pre-trained parameters) into a quantum device, along with a classical Mathematical optimization function. These circuits are very heavily dependent on the architecture of the proposed quantum device because parameter adjustments are adjusted based solely on the classical components within the device.^[87] Though the application is considerably infantile in the field of quantum machine learning, it has incredibly high promise for more efficiently generating efficient optimization functions.

Quantum learning theory

Quantum learning theory pursues a mathematical analysis of the quantum generalizations of classical learning models and of the possible speed-ups or other improvements that they may provide. The framework is very similar to that of classical computational learning theory, but the learner in this case is a quantum information processing device, while the data may be either classical or quantum. Quantum learning theory should be contrasted with the quantum-enhanced machine learning discussed above, where the goal was to consider specific problems and to use quantum protocols to improve the time complexity of classical algorithms for these problems. Although quantum learning theory is still under development, partial results in this direction have been obtained.^[88]

The starting point in learning theory is typically a concept class, a set of possible concepts. Usually a concept is a function on some domain, such as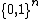

. For example, the concept class could be the set of disjunctive normal form (DNF) formulas on n bits or the set of Boolean circuits of some constant depth. The goal for the learner is to learn

(exactly or approximately) an unknown target concept from this concept class. The learner may be actively interacting with the target concept, or passively receiving samples from it.

In active learning, a learner can make membership queries to the target concept c, asking for its value c(x) on inputs x chosen by the learner. The learner then has to reconstruct the exact target concept, with high probability. In the model of quantum exact learning, the learner can make membership queries in quantum superposition. If the complexity of the learner is measured by the number of membership queries it makes, then quantum exact learners can be polynomially more efficient than classical learners for some concept classes, but not more.^[89] If complexity is measured by the amount of time

the learner uses, then there are concept classes that can be learned efficiently by

quantum learners but not by classical learners (under plausible complexity-theoretic assumptions).^[89]

A natural model of passive learning is Valiant's probably approximately correct (PAC) learning. Here the learner receives random examples (x,c(x)), where x is distributed according to some unknown distribution D. The learner's goal is to output a hypothesis function h such that h(x)=c(x) with high probability when x is drawn according to D. The learner has to be able to produce such an 'approximately correct' h for every D and every target concept c in its concept class.

We can consider replacing the random examples by potentially more powerful quantum examples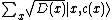

. In the PAC model (and the related agnostic model), this doesn't significantly reduce the number of examples needed: for every concept class, classical and

quantum sample complexity are the same up to constant factors.^[90] However, for learning under some

fixed distribution D, quantum examples can be very helpful, for example for learning DNF under

the uniform distribution.^[91] When considering time complexity, there exist concept classes that can be PAC-learned efficiently by quantum learners, even from classical examples, but not by classical learners (again, under plausible complexity-theoretic assumptions).^[89]

This passive learning type is also the most common scheme in supervised learning: a learning algorithm typically takes the training examples fixed, without the ability to query the label of unlabelled examples. Outputting a hypothesis h is a step of induction. Classically, an inductive model splits into a training and an application phase: the model parameters are estimated in the training phase, and the learned model is applied an arbitrary many times in the application phase. In the asymptotic limit of the number of applications, this splitting of phases is also present with quantum resources.^[92]

Implementations and experiments

The earliest experiments were conducted using the adiabatic D-Wave quantum computer, for instance, to detect cars in digital images using regularized boosting with a nonconvex objective function in a demonstration in 2009.^[93] Many experiments followed on the same architecture, and leading tech companies have shown interest in the potential of quantum machine learning for future technological implementations. In 2013, Google Research, NASA, and the Universities Space Research Association launched the Quantum Artificial Intelligence Lab which explores the use of the adiabatic D-Wave quantum computer.^[94]^[95] A more recent example trained a probabilistic generative models with arbitrary pairwise connectivity, showing that their model is capable of generating handwritten digits as well as reconstructing noisy images of bars and stripes and handwritten digits.^[50]

Using a different annealing technology based on nuclear magnetic resonance (NMR), a quantum Hopfield network was implemented in 2009 that mapped the input data and memorized data to Hamiltonians, allowing the use of adiabatic quantum computation.^[96] NMR technology also enables universal quantum computing{{Citation needed|date=February 2017}}, and it was used for the first experimental implementation of a quantum support vector machine to distinguish hand written number ‘6’ and ‘9’ on a liquid-state quantum computer in 2015.^[97] The training data involved the pre-processing of the image which maps them to normalized 2-dimensional vectors to represent the images as the states of a qubit. The two entries of the vector are the vertical and horizontal ratio of the pixel intensity of the image. Once the vectors are defined on the feature space, the quantum support vector machine was implemented to classify the unknown input vector. The readout avoids costly quantum tomography by reading out the final state in terms of direction (up/down) of the NMR signal.

Photonic implementations are attracting more attention,^[98] not the least because they do not require extensive cooling. Simultaneous spoken digit and speaker recognition and chaotic time-series prediction were demonstrated at data rates beyond 1 gigabyte per second in 2013.^[99] Using non-linear photonics to implement an all-optical linear classifier, a perceptron model was capable of learning the classification boundary iteratively from training data through a feedback rule.^[100] A core building block in many learning algorithms is to calculate the distance between two vectors: this was first experimentally demonstrated for up to eight dimensions using entangled qubits in a photonic quantum computer in 2015.^[101]

Recently, based on a neuromimetic approach, a novel ingredient has been added to the field of quantum machine learning, in the form of a so-called quantum memristor, a quantized model of the standard classical memristor.^[102] This device can be constructed by means of a tunable resistor, weak measurements on the system, and a classical feed-forward mechanism. An implementation of a quantum memristor in superconducting circuits has been proposed,^[103] and an experiment with quantum dots performed.^[104] A quantum memristor would implement nonlinear interactions in the quantum dynamics which would aid the search for a fully functional quantum neural network.

Since 2016, IBM has launced on online cloud-based platform for quantum software developers, called the IBM Q Experience. This platform consists of several fully operational quantum processors accessible via the IBM Web API. In doing so, the company is encouraging software developers to pursue new algorithms through a development environment with quantum capabilities. New architectures are being explored on an experimental basis, up to 32 qbits, utilizing both trapped-ion and superconductive quantum computing methods.

See also

References

1. ^{{Cite book|title=Supervised Learning with Quantum Computers|doi=10.1007/978-3-319-96424-9|series=Quantum Science and Technology|year=2018|last1=Schuld|first1=Maria|last2=Petruccione|first2=Francesco|isbn=978-3-319-96423-2}}
2. ^¹{{cite journal |doi=10.1080/00107514.2014.964942 |arxiv=1409.3097 |title=An introduction to quantum machine learning |journal=Contemporary Physics |volume=56 |issue=2 |pages=172–185 |year=2014 |last1=Schuld |first1=Maria |last2=Sinayskiy |first2=Ilya |last3=Petruccione |first3=Francesco |bibcode=2015ConPh..56..172S|citeseerx=10.1.1.740.5622 }}
3. ^{{cite book |last=Wittek |first=Peter |title=Quantum Machine Learning: What Quantum Computing Means to Data Mining |publisher=Academic Press |year=2014 |isbn=978-0-12-800953-6|url=http://www.sciencedirect.com/science/book/9780128009536}}
4. ^{{cite arxiv |eprint=1512.02900 |first1=Jeremy|last1=Adcock|first2=Euan|last2=Allen|first3=Matthew|last3=Day|first4=Stefan|last4=Frick|first5=Janna|last5=Hinchliff|first6=Mack|last6=Johnson|first7=Sam|last7=Morley-Short|first8=Sam|last8=Pallister|first9=Alasdair|last9=Price|first10=Stasja|last10=Stanisic|title=Advances in quantum machine learning |class=quant-ph |year=2015}}
5. ^{{Cite journal|arxiv=1611.09347 |first1=Jacob|last1=Biamonte|first2=Peter|last2=Wittek|first3=Nicola|last3=Pancotti|first4=Patrick|last4=Rebentrost|first5=Nathan|last5=Wiebe|first6=Seth|last6=Lloyd|title=Quantum machine learning |journal=Nature|volume=549|issue=7671|pages=195–202|year=2017|doi=10.1038/nature23474|pmid=28905917|bibcode=2017Natur.549..195B}}
6. ^{{Cite journal |first1=Alejandro|last1=Perdomo-Ortiz|first2=Marcello|last2=Benedetti|first3=John|last3=Realpe-Gómez|first4=Rupak|last4=Biswas|title=Opportunities and challenges for quantum-assisted machine learning in near-term quantum computers |journal=Quantum Science and Technology|volume=3|pages=030502|year=2018|doi=10.1088/2058-9565/aab859}}
7. ^¹{{Cite journal |arxiv=1401.2142 |last1=Wiebe |first1=Nathan |title=Quantum Algorithms for Nearest-Neighbor Methods for Supervised and Unsupervised Learning |journal=Quantum Information & Computation |volume=15 |issue=3 |pages=0318–0358 |last2=Kapoor |first2=Ashish |last3=Svore |first3=Krysta |year=2014|bibcode=2014arXiv1401.2142W }}
8. ^{{cite arxiv |eprint=1307.0411 |last1=Lloyd |first1=Seth |title=Quantum algorithms for supervised and unsupervised machine learning |last2=Mohseni |first2=Masoud |last3=Rebentrost |first3=Patrick |class=quant-ph |year=2013}}
9. ^{{Cite journal |arxiv=1303.6055 |last1=Yoo |first1=Seokwon |title=A quantum speedup in machine learning: Finding a N-bit Boolean function for a classification |journal=New Journal of Physics |volume=16 |issue=10 |pages=103014 |last2=Bang |first2=Jeongho |last3=Lee |first3=Changhyoup |last4=Lee |first4=Jinhyoung |year=2014 |doi=10.1088/1367-2630/16/10/103014|bibcode=2014NJPh...16j3014Y }}
10. ^{{Cite journal |arxiv=1706.01561 |last1=Lee|first1=Joong-Sung|last2=Bang|first2=Jeongho|last3=Hong|first3=Sunghyuk|last4=Lee|first4=Changhyoup|last5=Seol|first5=Kang Hee|last6=Lee|first6=Jinhyoung|last7=Lee|first7=Kwang-Geol|title=Experimental demonstration of quantum learning speedup with classical input data|journal=Physical Review A|volume=99|issue=1|pages=012313|year=2019|doi=10.1103/PhysRevA.99.012313}}
11. ^{{Cite journal|last=Schuld|first=Maria|last2=Sinayskiy|first2=Ilya|last3=Petruccione|first3=Francesco|date=2014-10-15|title=An introduction to quantum machine learning|journal=Contemporary Physics|language=en|volume=56|issue=2|pages=172–185|doi=10.1080/00107514.2014.964942|issn=0010-7514|citeseerx=10.1.1.740.5622}}
12. ^{{Cite journal|last=Benedetti|first=Marcello|last2=Realpe-Gómez|first2=John|last3=Biswas|first3=Rupak|last4=Perdomo-Ortiz|first4=Alejandro|date=2017-11-30|title=Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models|arxiv=1609.02542|journal=Physical Review X|volume=7|issue=4|pages=041052|doi=10.1103/PhysRevX.7.041052|issn=2160-3308}}
13. ^{{cite arxiv|last=Farhi|first=Edward|last2=Neven|first2=Hartmut|date=2018-02-16|title=Classification with Quantum Neural Networks on Near Term Processors|eprint=1802.06002|class=quant-ph}}
14. ^{{cite arxiv|last=Schuld|first=Maria|last2=Bocharov|first2=Alex|last3=Svore|first3=Krysta|last4=Wiebe|first4=Nathan|date=2018-04-02|title=Circuit-centric quantum classifiers|eprint=1804.00633|class=quant-ph}}
15. ^{{cite arxiv|last=Yu|first=Shang|last2=Albarran-Arriagada|first2=F.|last3=Retamal|first3=J. C.|last4=Wang|first4=Yi-Tao|last5=Liu|first5=Wei|last6=Ke|first6=Zhi-Jin|last7=Meng|first7=Yu|last8=Li|first8=Zhi-Peng|last9=Tang|first9=Jian-Shun|date=2018-08-28|title=Reconstruction of a Photonic Qubit State with Quantum Reinforcement Learning|eprint=1808.09241|class=quant-ph}}
16. ^{{cite arxiv|last=Broecker|first=Peter|last2=Assaad|first2=Fakher F.|last3=Trebst|first3=Simon|date=2017-07-03|title=Quantum phase recognition via unsupervised machine learning|eprint=1707.00663|class=cond-mat.str-el}}
17. ^{{Cite journal|last=Huembeli|first=Patrick|last2=Dauphin|first2=Alexandre|last3=Wittek|first3=Peter|year=2018|title=Identifying Quantum Phase Transitions with Adversarial Neural Networks|arxiv=1710.08382|journal=Physical Review B|volume=97|issue=13|pages=134109|doi=10.1103/PhysRevB.97.134109|issn=2469-9950}}
18. ^¹{{Cite journal|last=Krenn|first=Mario|date=2016-01-01|title=Automated Search for new Quantum Experiments|journal=Physical Review Letters|volume=116|issue=9|pages=090405|arxiv=1509.02749|bibcode=2016PhRvL.116i0405K|doi=10.1103/PhysRevLett.116.090405|pmid=26991161}}
19. ^¹{{Cite journal|last=Knott|first=Paul|date=2016-03-22|title=A search algorithm for quantum state engineering and metrology|journal=New Journal of Physics|volume=18|issue=7|pages=073033|arxiv=1511.05327|bibcode=2016NJPh...18g3033K|doi=10.1088/1367-2630/18/7/073033}}
20. ^{{Cite journal|last=Melnikov|first=Alexey A.|last2=Nautrup|first2=Hendrik Poulsen|last3=Krenn|first3=Mario|last4=Dunjko|first4=Vedran|last5=Tiersch|first5=Markus|last6=Zeilinger|first6=Anton|last7=Briegel|first7=Hans J.|year=1221|title=Active learning machine learns to create new quantum experiments|url=http://www.pnas.org/content/115/6/1221|journal=Proceedings of the National Academy of Sciences|language=en|volume=115|issue=6|pages=1221–1226|doi=10.1073/pnas.1714936115|issn=0027-8424|pmc=5819408|pmid=29348200|arxiv=1706.00868}}
21. ^{{cite arxiv|last=Huggins|first=William|last2=Patel|first2=Piyush|last3=Whaley|first3=K. Birgitta|last4=Stoudenmire|first4=E. Miles|date=2018-03-30|title=Towards Quantum Machine Learning with Tensor Networks|eprint=1803.11537|class=quant-ph}}
22. ^{{cite arxiv|last=Carleo|first=Giuseppe|last2=Nomura|first2=Yusuke|last3=Imada|first3=Masatoshi|date=2018-02-26|title=Constructing exact representations of quantum many-body systems with deep neural networks|eprint=1802.09558|class=cond-mat.dis-nn}}
23. ^{{cite arxiv|last=Bény|first=Cédric|date=2013-01-14|title=Deep learning and the renormalization group|eprint=1301.3124 |class=quant-ph}}
24. ^{{cite arxiv|last=Arunachalam|first=Srinivasan|last2=de Wolf|first2=Ronald|date=2017-01-24|title=A Survey of Quantum Learning Theory|eprint=1701.06806|class=quant-ph}}
25. ^{{Cite book|title=Machine Learning in a Quantum World|last=Aïmeur|first=Esma|last2=Brassard|first2=Gilles|last3=Gambs|first3=Sébastien|date=2006-06-07|journal=Advances in Artificial Intelligence|isbn=978-3-540-34628-9|series=Lecture Notes in Computer Science|volume=4013|pages=431–442|language=en|doi=10.1007/11766247_37}}
26. ^¹²{{Cite journal|last=Dunjko|first=Vedran|last2=Taylor|first2=Jacob M.|last3=Briegel|first3=Hans J.|date=2016-09-20|title=Quantum-Enhanced Machine Learning|journal=Physical Review Letters|volume=117|issue=13|pages=130501|arxiv=1610.08251|bibcode=2016PhRvL.117m0501D|doi=10.1103/PhysRevLett.117.130501|pmid=27715099}}
27. ^¹{{cite journal |doi=10.1103/PhysRevLett.113.130503|pmid=25302877|title=Quantum Support Vector Machine for Big Data Classification|journal=Physical Review Letters|volume=113|issue=13|pages=130503|year=2014|last1=Rebentrost|first1=Patrick|last2=Mohseni|first2=Masoud|last3=Lloyd|first3=Seth|bibcode=2014PhRvL.113m0503R|arxiv=1307.0471|hdl=1721.1/90391}}
28. ^¹{{cite journal |doi=10.1103/PhysRevLett.109.050505|pmid=23006156|title=Quantum Algorithm for Data Fitting|journal=Physical Review Letters|volume=109|issue=5|pages=050505|year=2012|last1=Wiebe|first1=Nathan|last2=Braun|first2=Daniel|last3=Lloyd|first3=Seth|bibcode=2012PhRvL.109e0505W|arxiv=1204.5242}}
29. ^¹{{cite journal |doi=10.1103/PhysRevA.94.022342|title=Prediction by linear regression on a quantum computer|journal=Physical Review A|volume=94|issue=2|pages=022342|year=2016|last1=Schuld|first1=Maria|last2=Sinayskiy|first2=Ilya|last3=Petruccione|first3=Francesco|bibcode=2016PhRvA..94b2342S|arxiv=1601.07823}}
30. ^¹{{cite arxiv |eprint=1512.03929 |last1=Zhao |first1=Zhikuan |title=Quantum assisted Gaussian process regression |last2=Fitzsimons |first2=Jack K. |last3=Fitzsimons |first3=Joseph F. |class=quant-ph |year=2015}}
31. ^{{Cite journal |arxiv=0811.3171 |last1=Harrow |first1=Aram W. |title=Quantum algorithm for solving linear systems of equations |journal=Physical Review Letters |volume=103 |issue=15 |pages=150502 |last2=Hassidim |first2=Avinatan |last3=Lloyd |first3=Seth |year=2008 |doi=10.1103/PhysRevLett.103.150502|pmid=19905613 |bibcode=2009PhRvL.103o0502H }}
32. ^{{cite conference |url= |title=Hamiltonian simulation with nearly optimal dependence on all parameters |last1=Berry |first1= Dominic W.|last2=Childs |first2=Andrew M.|last3=Kothari|first3=Robin|date=2015 |publisher=IEEE |pages=792–809 |conference= 56th Annual Symposium on Foundations of Computer Science|doi=10.1109/FOCS.2015.54|arxiv=1501.01715}}
33. ^{{cite journal |doi=10.1038/nphys3029|title=Quantum principal component analysis|journal=Nature Physics|volume=10|issue=9|pages=631|year=2014|last1=Lloyd|first1=Seth|last2=Mohseni|first2=Masoud|last3=Rebentrost|first3=Patrick|bibcode=2014NatPh..10..631L|arxiv=1307.0401|citeseerx=10.1.1.746.480}}
34. ^{{cite journal |doi=10.1103/PhysRevA.73.012307|title=Efficient state preparation for a register of quantum bits|journal=Physical Review A|volume=73|issue=1|pages=012307|year=2006|last1=Soklakov|first1=Andrei N.|last2=Schack|first2=Rüdiger|bibcode=2006PhRvA..73a2307S|arxiv=quant-ph/0408045}}
35. ^{{cite journal |doi=10.1103/PhysRevLett.100.160501|pmid=18518173|title=Quantum Random Access Memory|journal=Physical Review Letters|volume=100|issue=16|pages=160501|year=2008|last1=Giovannetti|first1=Vittorio|last2=Lloyd|first2=Seth|last3=MacCone|first3=Lorenzo|bibcode=2008PhRvL.100p0501G|arxiv=0708.1879}}
36. ^{{Cite journal |doi=10.1038/nphys3272|title=Read the fine print|journal=Nature Physics|volume=11|issue=4|pages=291–293|year=2015|last1=Aaronson|first1=Scott|bibcode=2015NatPh..11..291A}}
37. ^{{Cite journal |doi=10.1103/PhysRevA.99.012326|title=Optimal usage of quantum random access memory in quantum machine learning|journal=Physical Review A|volume=99|issue=1|pages=012326|year=2019|last1=Bang|first1=Jeongho|last2=Dutta|first2=Arijit|last3=Lee|first3=Seung-Woo|last4=Kim|first4=Jaewan}}
38. ^{{Cite journal|last=Aïmeur|first=Esma|last2=Brassard|first2=Gilles|last3=Gambs|first3=Sébastien|date=2013-02-01|title=Quantum speed-up for unsupervised learning|journal=Machine Learning|language=en|volume=90|issue=2|pages=261–287|doi=10.1007/s10994-012-5316-5|issn=0885-6125}}
39. ^{{cite conference |arxiv=1602.04799|last1=Wiebe|first1=Nathan|title=Quantum Perceptron Models|last2=Kapoor|first2=Ashish|last3=Svore|first3=Krysta M.|conference=Advances in Neural Information Processing Systems|volume=29||pages=3999–4007|url=https://papers.nips.cc/paper/6401-quantum-perceptron-models||bibcode=2016arXiv160204799W|year=2016}}
40. ^{{cite journal |doi= 10.1038/srep00444|pmid= 22685626|pmc= 3370332|title= Google in a Quantum Network|journal= Scientific Reports|volume= 2|issue= 444|pages= 444|year= 2012|last1= Paparo|first1= Giuseppe Davide|last2= Martin-Delgado|first2= Miguel Angel|bibcode= 2012NatSR...2E.444P|arxiv= 1112.2079}}
41. ^¹²{{cite journal |doi=10.1103/PhysRevX.4.031002|title=Quantum Speedup for Active Learning Agents|journal=Physical Review X|volume=4|issue=3|pages=031002|year=2014|last1=Paparo|first1=Giuseppe Davide|last2=Dunjko|first2=Vedran|last3=Makmal|first3=Adi|last4=Martin-Delgado|first4=Miguel Angel|last5=Briegel|first5=Hans J.|bibcode=2014PhRvX...4c1002P|arxiv=1401.4997}}
42. ^{{Cite journal|last2=Chen|first2=Chunlin|last3=Li|first3=Hanxiong|last4=Tarn|first4=Tzyh-Jong|year=2008|title=Quantum Reinforcement Learning|journal=IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics)|volume=38|issue=5|pages=1207–1220|doi=10.1109/TSMCB.2008.925743|pmid=18784007|first1=Daoyi|last1=Dong|arxiv=0810.3828|citeseerx=10.1.1.243.5369}}
43. ^{{cite arxiv|eprint=1612.05695|last1=Crawford|first1=Daniel|title=Reinforcement Learning Using Quantum Boltzmann Machines|last2=Levit|first2=Anna|last3=Ghadermarzy|first3=Navid|last4=Oberoi|first4=Jaspreet S.|last5=Ronagh|first5=Pooya|class=quant-ph|year=2018}}
44. ^{{Cite journal|last=Briegel|first=Hans J.|last2=Cuevas|first2=Gemma De las|date=2012-05-15|title=Projective simulation for artificial intelligence|url=http://www.nature.com/articles/srep00400|journal=Scientific Reports|language=en|volume=2|issue=400|pages=400|doi=10.1038/srep00400|issn=2045-2322|pmc=3351754|pmid=22590690|arxiv=1104.3787|bibcode=2012NatSR...2E.400B}}
45. ^{{cite journal|last1=Lamata|first1=Lucas|title=Basic protocols in quantum reinforcement learning with superconducting circuits|journal=Scientific Reports|volume=7|issue=1|pages=1609|doi=10.1038/s41598-017-01711-6|pmid=28487535|pmc=5431677|year=2017|arxiv=1701.05131|bibcode=2017NatSR...7.1609L}}
46. ^{{Cite journal|last=Dunjko|first=V.|last2=Friis|first2=N.|last3=Briegel|first3=H. J.|date=2015-01-01|title=Quantum-enhanced deliberation of learning agents using trapped ions|url=http://stacks.iop.org/1367-2630/17/i=2/a=023006|journal=New Journal of Physics|language=en|volume=17|issue=2|pages=023006|doi=10.1088/1367-2630/17/2/023006|issn=1367-2630|arxiv=1407.2830|bibcode=2015NJPh...17b3006D}}
47. ^{{Cite journal|last=Sriarunothai|first=Th.|last2=Wölk|first2=S.|last3=Giri|first3=G. S.|last4=Friis|first4=N.|last5=Dunjko|first5=V.|last6=Briegel|first6=H. J.|last7=Wunderlich|first7=Ch.|date=2019|title=Speeding-up the decision making of a learning agent using an ion trap quantum processor|url=http://iopscience.iop.org/article/10.1088/2058-9565/aaef5e|journal=Quantum Science and Technology|language=en|volume=4|issue=1|pages=015014|doi=10.1088/2058-9565/aaef5e|issn=2058-9565}}
48. ^{{cite journal |last1=Biswas |first1=Rupak |last2=Jiang |first2=Zhang |last3=Kechezi |first3=Kostya |last4=Knysh |first4=Sergey |last5=Mandrà |first5=Salvatore |last6=O’Gorman |first6=Bryan |last7=Perdomo-Ortiz |first7=Alejando |last8=Pethukov |first8=Andre |last9=Realpe-Gómez |first9=John |last10=Rieffel |first10=Eleanor|author1-link= Eleanor Rieffel |last11=Venturelli|first11=Davide|last12=Vasko|first12=Fedir|last13=Wang|first13=Zhihui |title=A NASA perspective on quantum computing: Opportunities and challenges |year=2016|doi=10.1016/j.parco.2016.11.002|journal=Parallel Computing|volume=64 |pages=81–98 |url=https://zenodo.org/record/1259293 }}
49. ^¹{{cite arXiv |last1=Adachi |first1=Steven H. |last2=Henderson |first2=Maxwell P. |date=2015 |title=Application of quantum annealing to training of deep neural networks |eprint=1510.06356 |class=quant-ph}}
50. ^¹²³{{Cite journal|last1=Benedetti |first1=Marcello |last2=Realpe-Gómez |first2=John |last3=Biswas |first3=Rupak |last4=Perdomo-Ortiz |first4=Alejandro |year=2017 |title=Quantum-assisted learning of graphical models with arbitrary pairwise connectivity |journal=Physical Review X |volume=7 |issue=4 |pages=041052 |arxiv=1609.02542 |doi=10.1103/PhysRevX.7.041052 |bibcode=2017PhRvX...7d1052B }}
51. ^¹{{cite journal |last1=Benedetti |first1=Marcello |last2=Realpe-Gómez |first2=John |last3=Biswas |first3=Rupak |last4=Perdomo-Ortiz |first4=Alejandro |date=2016 |title=Estimation of effective temperatures in quantum annealers for sampling applications: A case study with possible applications in deep learning |journal=Physical Review A |doi=10.1103/PhysRevA.94.022308 |volume=94 |issue=2 |pages=022308 |bibcode=2016PhRvA..94b2308B|arxiv=1510.07611 }}
52. ^¹{{cite arXiv |last1=Korenkevych |first1=Dmytro |last2=Xue |first2=Yanbo |last3=Bian |first3=Zhengbing |last4=Chudak |first4=Fabian |last5=Macready |first5=William G. |last6=Rolfe |first6=Jason |last7=Andriyash |first7=Evgeny |date=2016 |title=Benchmarking quantum hardware for training of fully visible Boltzmann machines |eprint=1611.04528 |class=quant-ph}}
53. ^{{Cite journal |last1=Amin |first1=Mohammad H. |last2=Andriyash |first2=Evgeny |last3=Rolfe |first3=Jason |last4=Kulchytskyy |first4=Bohdan |last5=Melko |first5=Roger |year=2018 |title=Quantum Boltzmann machines |journal=Phys. Rev. X |volume=8 |issue=21050 |pages=021050 |arxiv=1601.02036 |doi=10.1103/PhysRevX.8.021050 }}
54. ^{{Cite web|url=https://archive.is/jzQ7n|title=Phys. Rev. E 72, 026701 (2005): Quantum annealing in a kinetically co…|date=2014-01-13|website=archive.is|access-date=2018-12-07}}
55. ^{{cite arXiv |last1=Wiebe |first1=Nathan |last2=Kapoor |first2=Ashish |last3=Svore |first3=Krysta M. |date=2014 |title=Quantum deep learning |eprint=1412.3489 |class=quant-ph}}
56. ^{{cite journal |last1=Wittek |first1=Peter |last2=Gogolin |first2=Christian |date=2017 |title=Quantum Enhanced Inference in Markov Logic Networks |journal=Scientific Reports|doi=10.1038/srep45672|pmid=28422093 |pmc=5395824 |volume=7|issue=45672 |page=45672 |arxiv=1611.08104|bibcode=2017NatSR...745672W}}
57. ^¹²³{{Cite journal|date=2001-11-01|title=Quantum Neural Networks|url=https://www.sciencedirect.com/science/article/pii/S0022000001917696|journal=Journal of Computer and System Sciences|language=en|volume=63|issue=3|pages=355–383|doi=10.1006/jcss.2001.1769|issn=0022-0000|last1=Gupta|first1=Sanjay|last2=Zia|first2=R.K.P.}}
58. ^¹{{Citation|last=Ezhov|first=Alexandr A.|title=Quantum Neural Networks|date=2000|work=Future Directions for Intelligent Systems and Information Sciences|pages=213–235|publisher=Physica-Verlag HD|language=en|doi=10.1007/978-3-7908-1856-7_11|isbn=9783790824704|last2=Ventura|first2=Dan|citeseerx=10.1.1.683.5972}}
59. ^¹{{Cite journal|date=2000-10-01|title=Simulations of quantum neural networks|url=https://www.sciencedirect.com/science/article/pii/S0020025500000566|journal=Information Sciences|language=en|volume=128|issue=3–4|pages=257–269|doi=10.1016/S0020-0255(00)00056-6|issn=0020-0255|last1=Behrman|first1=E.C.|last2=Nash|first2=L.R.|last3=Steck|first3=J.E.|last4=Chandrashekar|first4=V.G.|last5=Skinner|first5=S.R.}}
60. ^{{cite book|last1=Clark|first1=Lewis A.|last2=Huang W.|first2=Wei|last3=Barlow|first3=Thomas H.|last4=Beige|first4=Almut|editor1-last=Sanayei|editor1-first=Ali|editor2-last=Rössler|editor2-first=Otto E.|editor3-last=Zelinka|editor3-first=Ivan|title=ISCS 2014: Interdisciplinary Symposium on Complex Systems. Emergence, Complexity and Computation|journal=Iscs , P. 143, Springer (2015)|volume=14|issue=14|isbn=978-3-319-10759-2|pages=131–151|chapter=Hidden Quantum Markov Models and Open Quantum Systems with Instantaneous Feedback|arxiv=1406.5847|doi=10.1007/978-3-319-10759-2_16|series=Emergence, Complexity and Computation|year=2015|citeseerx=10.1.1.749.3332}}
61. ^¹²{{Cite journal|last=Srinivasan|first=Siddarth|last2=Gordon|first2=Geoff|last3=Boots|first3=Byron|date=2018|title=Learning Hidden Quantum Markov Models|url=https://www.cc.gatech.edu/~bboots3/files/learning_hqmms.pdf|journal=Aistats|volume=|pages=|via=}}
62. ^{{cite journal|last1=Sentís|first1=Gael|last2=Guţă|first2=Mădălin|last3=Adesso|first3=Gerardo|date=9 July 2015|title=Quantum learning of coherent states|journal=EPJ Quantum Technology|volume=2|issue=1|doi=10.1140/epjqt/s40507-015-0030-4}}
63. ^{{cite journal|last1=Sasaki|first1=Masahide|last2=Carlini|first2=Alberto|date=6 August 2002|title=Quantum learning and universal quantum matching machine|journal=Physical Review A|volume=66|issue=2|pages=022303|arxiv=quant-ph/0202173|bibcode=2002PhRvA..66b2303S|doi=10.1103/PhysRevA.66.022303}}
64. ^{{cite journal|last1=Bisio|first1=Alessandro|last2=Chiribella|first2=Giulio|last3=D’Ariano|first3=Giacomo Mauro|last4=Facchini|first4=Stefano|last5=Perinotti|first5=Paolo|date=25 March 2010|title=Optimal quantum learning of a unitary transformation|journal=Physical Review A|volume=81|issue=3|pages=032324|arxiv=0903.0543|bibcode=2010PhRvA..81c2324B|doi=10.1103/PhysRevA.81.032324}}
65. ^{{Cite book|title=Quantum Clustering Algorithms|last1=Aïmeur|first1=Esma|last2=Brassard|first2=Gilles|last3=Gambs|first3=Sébastien|date=1 January 2007|journal=Proceedings of the 24th International Conference on Machine Learning|isbn=9781595937933|pages=1–8|citeseerx=10.1.1.80.9513|doi=10.1145/1273496.1273497}}
66. ^¹{{cite journal|last1=Sentís|first1=Gael|last2=Calsamiglia|first2=John|last3=Muñoz-Tapia|first3=Raúl|last4=Bagan|first4=Emilio|year=2012|title=Quantum learning without quantum memory|url=|journal=Scientific Reports|volume=2|issue=|page=708|arxiv=1106.2742|bibcode=2012NatSR...2E.708S|doi=10.1038/srep00708|pmc=3464493|pmid=23050092}}
67. ^{{cite journal|last1=Wiebe|first1=Nathan|last2=Granade|first2=Christopher|last3=Ferrie|first3=Christopher|last4=Cory|first4=David|year=2014|title=Quantum Hamiltonian learning using imperfect quantum resources|url=|journal=Physical Review A|volume=89|issue=4|page=042314|arxiv=1311.5269|bibcode=2014PhRvA..89d2314W|doi=10.1103/physreva.89.042314|hdl=10453/118943}}
68. ^¹{{Cite journal|last1=Bisio|first1=Alessandro|last2=Chiribella|first2=Giulio|last3=D'Ariano|first3=Giacomo Mauro|last4=Facchini|first4=Stefano|last5=Perinotti|first5=Paolo|year=2010|title=Optimal quantum learning of a unitary transformation|journal=Physical Review A|volume=81|issue=3|pages=032324|arxiv=0903.0543|bibcode=2010PhRvA..81c2324B|doi=10.1103/PhysRevA.81.032324}}
69. ^¹{{cite journal|last1=Jeongho|last2=Junghee Ryu|first2=Bang|last3=Yoo|first3=Seokwon|last4=Pawłowski|first4=Marcin|last5=Lee|first5=Jinhyoung|year=2014|title=A strategy for quantum algorithm design assisted by machine learning|url=|journal=New Journal of Physics|volume=16|issue=1|page=073017|arxiv=1304.2169|bibcode=2014NJPh...16a3017K|doi=10.1088/1367-2630/16/1/013017}}
70. ^{{Cite journal|last=Granade|first=Christopher E.|last2=Ferrie|first2=Christopher|last3=Wiebe|first3=Nathan|last4=Cory|first4=D. G.|date=2012-10-03|title=Robust Online Hamiltonian Learning|journal=New Journal of Physics|volume=14|issue=10|pages=103013|arxiv=1207.1655|bibcode=2012NJPh...14j3013G|doi=10.1088/1367-2630/14/10/103013|issn=1367-2630}}
71. ^{{Cite journal|last=Wiebe|first=Nathan|last2=Granade|first2=Christopher|last3=Ferrie|first3=Christopher|last4=Cory|first4=D. G.|year=2014|title=Hamiltonian Learning and Certification Using Quantum Resources|journal=Physical Review Letters|volume=112|issue=19|pages=190501|arxiv=1309.0876|bibcode=2014PhRvL.112s0501W|doi=10.1103/PhysRevLett.112.190501|issn=0031-9007|pmid=24877920}}
72. ^{{Cite journal|last=Wiebe|first=Nathan|last2=Granade|first2=Christopher|last3=Ferrie|first3=Christopher|last4=Cory|first4=David G.|date=2014-04-17|title=Quantum Hamiltonian Learning Using Imperfect Quantum Resources|journal=Physical Review A|volume=89|issue=4|pages=042314|arxiv=1311.5269|bibcode=2014PhRvA..89d2314W|doi=10.1103/PhysRevA.89.042314|issn=1050-2947|hdl=10453/118943}}
73. ^{{Cite journal|last=Sasaki|first=Madahide|last2=Carlini|first2=Alberto|last3=Jozsa|first3=Richard|date=2001|title=Quantum Template Matching|journal=Physical Review A|volume=64|issue=2|pages=022317|arxiv=quant-ph/0102020|bibcode=2001PhRvA..64b2317S|doi=10.1103/PhysRevA.64.022317}}
74. ^{{Cite journal|last=Sasaki|first=Masahide|date=2002|title=Quantum learning and universal quantum matching machine|journal=Physical Review A|volume=66|issue=2|pages=022303|arxiv=quant-ph/0202173|bibcode=2002PhRvA..66b2303S|doi=10.1103/PhysRevA.66.022303}}
75. ^{{Cite journal|last=Sentís|first=Gael|last2=Guţă|first2=Mădălin|last3=Adesso|first3=Gerardo|date=2015-07-09|title=Quantum learning of coherent states|journal=EPJ Quantum Technology|language=en|volume=2|issue=1|pages=17|doi=10.1140/epjqt/s40507-015-0030-4|issn=2196-0763}}
76. ^{{Cite journal|last=Lee|first=Sang Min|last2=Lee|first2=Jinhyoung|last3=Bang|first3=Jeongho|date=2018-11-02|title=Learning unknown pure quantum states|journal=Physical Review A|language=en|volume=98|issue=5|pages=052302|doi=10.1103/PhysRevA.98.052302}}
77. ^{{Cite journal|last=Zahedinejad|first=Ehsan|last2=Ghosh|first2=Joydip|last3=Sanders|first3=Barry C.|date=2016-11-16|title=Designing High-Fidelity Single-Shot Three-Qubit Gates: A Machine Learning Approach|journal=Physical Review Applied|volume=6|issue=5|pages=054005|arxiv=1511.08862|bibcode=2016PhRvP...6e4005Z|doi=10.1103/PhysRevApplied.6.054005|issn=2331-7019}}
78. ^{{Cite journal|last=Banchi|first=Leonardo|last2=Pancotti|first2=Nicola|last3=Bose|first3=Sougato|date=2016-07-19|title=Quantum gate learning in qubit networks: Toffoli gate without time-dependent control|url=http://www.nature.com/articles/npjqi201619|journal=npj Quantum Information|volume=2|pages=16019|bibcode=2016npjQI...216019B|doi=10.1038/npjqi.2016.19}}
79. ^{{Cite journal|last=von Lilienfeld|first=O. Anatole|date=2018-04-09|title=Quantum Machine Learning in Chemical Compound Space|journal=Angewandte Chemie International Edition|volume=57|issue=16|pages=4164|doi=10.1002/anie.201709686}}
80. ^{{Cite journal|last=Bartok|first=Albert P.|last2=Payne|first2=Mike C.|last3=Risi|first3=Kondor|last4=Csanyi|first4=Gabor|date=2010|title=Gaussian approximation potentials: The accuracy of quantum mechanics, without the electrons|journal=Physical Review Letters|volume=104|issue=13|pages=136403|doi=10.1103/PhysRevLett.104.136403}}
81. ^{{Cite journal|last=Rupp|first=Matthias|last2=Tkatchenko|first2=Alexandre|last3=Muller|first3=Klaus-Robert|last4=von Lilienfeld|first4=O. Anatole|date=2012-01-31|title=Fast and Accurate Modeling of Molecular Atomization Energies With Machine Learning|journal=Physical Review Letters|volume=355|issue=6325|pages=602|arxiv=1109.2618|bibcode=2012PhRvL.108e8301R|doi=10.1103/PhysRevLett.108.058301|pmid=22400967}}
82. ^{{Cite journal|last=Xia|first=Rongxin|last2=Kais|first2=Sabre|date=2018-10-10|title=Quantum machine learning for electronic structure calculations|journal=Nature Communications|volume=9|pages=4195|doi=10.1038/s41467-018-06598-z}}
83. ^{{Cite journal|last=Carleo|first=Giuseppe|last2=Troyer|first2=Matthias|date=2017-02-09|title=Solving the quantum many-body problem with artificial neural networks|url=http://science.sciencemag.org/content/355/6325/602|journal=Science|volume=355|issue=6325|pages=602–606|arxiv=1606.02318|bibcode=2017Sci...355..602C|doi=10.1126/science.aag2302|pmid=28183973}}
84. ^{{Cite journal|last=van Nieuwenburg|first=Evert|last2=Liu|first2=Ye-Hua|last3=Huber|first3=Sebastian|year=2017|title=Learning phase transitions by confusion|url=http://www.nature.com/nphys/journal/vaop/ncurrent/full/nphys4037.html|journal=Nature Physics|volume=13|issue=5|pages=435|arxiv=1610.02048|bibcode=2017NatPh..13..435V|doi=10.1038/nphys4037|via=}}
85. ^{{Cite journal|last=Hentschel|first=Alexander|date=2010-01-01|title=Machine Learning for Precise Quantum Measurement|journal=Physical Review Letters|volume=104|issue=6|pages=063603|arxiv=0910.0762|bibcode=2010PhRvL.104f3603H|doi=10.1103/PhysRevLett.104.063603|pmid=20366821}}
86. ^{{Cite web|url=https://qmlt.readthedocs.io/en/latest/variational.html|title=Variational Circuits — Quantum Machine Learning Toolbox 0.7.1 documentation|website=qmlt.readthedocs.io|access-date=2018-12-06}}
87. ^{{Cite web|url=https://medium.com/xanaduai/quantum-machine-learning-1-0-76a525c8cf69|title=Quantum Machine Learning 1.0|last=Schuld|first=Maria|date=2018-06-12|website=XanaduAI|access-date=2018-12-07}}
88. ^{{cite arXiv|class=quant-ph|first2=Ronald|last2=de Wolf|title=A Survey of Quantum Learning Theory|date=2017|last1=Arunachalam|first1=Srinivasan|eprint=1701.06806}}
89. ^¹²{{cite journal|last2=Gortler|first2=Steven J.|year=2004|title=Equivalences and Separations Between Quantum and Classical Learnability|journal=SIAM Journal on Computing|volume=33|issue=5|pages=1067–1092|doi=10.1137/S0097539704412910|last1=Servedio|first1=Rocco A.|citeseerx=10.1.1.69.6555}}
90. ^{{cite arXiv|class=quant-ph|first2=Ronald|last2=de Wolf|title=Optimal Quantum Sample Complexity of Learning Algorithms|date=2016|last1=Arunachalam|first1=Srinivasan|eprint=1607.00932}}
91. ^{{cite journal|last2=Jeffrey|first2=Jackson C.|year=1999|title=Learning DNF over the Uniform Distribution Using a Quantum Example Oracle|journal=SIAM Journal on Computing|volume=28|issue=3|pages=1136–1153|doi=10.1137/S0097539795293123|last1=Nader|first1=Bshouty H.|citeseerx=10.1.1.23.5709}}
92. ^{{cite journal|first2=Gael|last2=Sentís|title=Inductive supervised quantum learning|year=2017|last1=Monràs|first1=Alex|last3=Wittek|first3=Peter|journal=Physical Review Letters|volume=118|issue=19|pages=190503|doi=10.1103/PhysRevLett.118.190503 |pmid=28548536|bibcode=2017PhRvL.118s0503M|arxiv=1605.07541}}
93. ^{{cite web|url=http://static.googleusercontent.com/media/www.google.com/de//googleblogs/pdfs/nips_demoreport_120709_research.pdf|title=NIPS 2009 Demonstration: Binary Classification using Hardware Implementation of Quantum Annealing|publisher=Static.googleusercontent.com|format=PDF|accessdate=26 November 2014}}
94. ^{{cite web|url=https://plus.google.com/+QuantumAILab|title=Google Quantum A.I. Lab Team|date=31 January 2017|website=Google Plus|access-date=31 January 2017|quote=|author=}}
95. ^{{cite web|url=https://ti.arc.nasa.gov/tech/dash/physics/quail/|title=NASA Quantum Artificial Intelligence Laboratory|date=31 January 2017|website=NASA|publisher=NASA|access-date=31 January 2017|quote=|author=}}
96. ^{{cite journal|last2=Neves|first2=Jorge L.|last3=Sollacher|first3=Rudolf|last4=Glaser|first4=Steffen J.|year=2009|title=Quantum pattern recognition with liquid-state nuclear magnetic resonance|journal=Physical Review A|volume=79|issue=4|pages=042321|arxiv=0802.1592|bibcode=2009PhRvA..79d2321N|doi=10.1103/PhysRevA.79.042321|last1=Neigovzen|first1=Rodion}}
97. ^{{cite journal|last2=Liu|first2=Xiaomei|last3=Xu|first3=Nanyang|last4=Du|first4=Jiangfeng|year=2015|title=Experimental Realization of a Quantum Support Vector Machine|journal=Physical Review Letters|volume=114|issue=14|pages=140504|arxiv=1410.1054|bibcode=2015PhRvL.114n0504L|doi=10.1103/PhysRevLett.114.140504|pmid=25910101|last1=Li|first1=Zhaokai}}
98. ^{{cite journal|last1=Wan|first1=Kwok-Ho|last2=Dahlsten|first2=Oscar|last3=Kristjansson|first3=Hler|last4=Gardner|first4=Robert|last5=Kim|first5=Myungshik|year=2017|title=Quantum generalisation of feedforward neural networks|journal=Npj Quantum Information|volume=3|issue=36|pages=36|arxiv=1612.01045|bibcode=2017npjQI...3...36W|doi=10.1038/s41534-017-0032-4}}
99. ^{{cite journal|last2=Soriano|first2=Miguel C.|last3=Mirasso|first3=Claudio R.|last4=Fischer|first4=Ingo|year=2013|title=Parallel photonic information processing at gigabyte per second data rates using transient states|journal=Nature Communications|volume=4|pages=1364|bibcode=2013NatCo...4E1364B|doi=10.1038/ncomms2368|pmc=3562454|pmid=23322052|last1=Brunner|first1=Daniel}}
100. ^{{cite journal|last2=Mabuchi|first2=Hideo|year=2015|title=A coherent perceptron for all-optical learning|journal=EPJ Quantum Technology|volume=2|arxiv=1501.01608|doi=10.1140/epjqt/s40507-015-0023-3|last1=Tezak|first1=Nikolas}}
101. ^{{cite journal|last2=Wu|first2=D.|last3=Su|first3=Z.-E.|last4=Chen|first4=M.-C.|last5=Wang|first5=X.-L.|last6=Li|first6=Li|last7=Liu|first7=N.-L.|last8=Lu|first8=C.-Y.|last9=Pan|first9=J.-W.|year=2015|title=Entanglement-Based Machine Learning on a Quantum Computer|journal=Physical Review Letters|volume=114|issue=11|pages=110504|arxiv=1409.7770|bibcode=2015PhRvL.114k0504C|doi=10.1103/PhysRevLett.114.110504|pmid=25839250|last1=Cai|first1=X.-D.}}
102. ^{{cite journal |doi=10.1038/srep29507 |pmid=27381511 |pmc=4933948 |title=Quantum memristors |journal=Scientific Reports |volume=6 |issue=2016 |pages=29507 |year=2016|last1=Pfeiffer |first1=P. |last2=Egusquiza |first2=I. L. |last3=Di Ventra |first3=M. |last4=Sanz |first4=M. |last5=Solano |first5=E. |bibcode=2016NatSR...629507P|arxiv=1511.02192 }}
103. ^{{cite journal |doi=10.1038/srep42044|pmid= 28195193|pmc= 5307327|last1= Salmilehto|first1= J.|title= Quantum Memristors with Superconducting Circuits|last2= Deppe|first2= F.|last3= Di Ventra|first3= M.|last4= Sanz|first4= M.|last5= Solano|first5= E.|journal=Scientific Reports |volume=7 |issue= 42044|pages=42044|year= 2017|arxiv=1603.04487|bibcode=2017NatSR...742044S}}
104. ^{{Cite journal|arxiv=1612.08409|last1=Li|first1=Ying|title=A simple and robust quantum memristor|journal=Physical Review B|volume=96|issue=7|pages=075446|last2= Holloway|first2=Gregory W.|last3= Benjamin|first3=Simon C.|last4= Briggs|first4=G. Andrew D.|last5=Baugh|first5=Jonathan|last6= Mol|first6=Jan A.|year=2017|doi=10.1103/PhysRevB.96.075446|bibcode=2017PhRvB..96g5446L}}

Machine learning with quantum computers