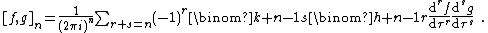“Rankin–Cohen bracket”的意思、由来-开放百科全书

词条

Rankin–Cohen bracket

释义

Definition
Representation theory
References

In mathematics, the Rankin–Cohen bracket of two modular forms is another modular form, generalizing the product of two modular forms.

{{harvs|txt|last=Rankin|authorlink=Robert Alexander Rankin|year=1956|year2=1957}} gave some general conditions for polynomials in derivatives of modular forms to be modular forms, and {{harvs|txt|last=Cohen|authorlink=Henri Cohen (number theorist)|year=1975}} found the explicit examples of such polynomials that give Rankin–Cohen brackets. They were named by {{harvs|txt||last=Zagier|year=1994}}, who introduced Rankin–Cohen algebras as an abstract setting for Rankin–Cohen brackets.

Definition

If and 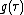are modular form of weight k and h respectively then their nth Rankin–Cohen bracket [f,g]_n is given by

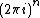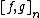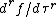It is a modular form of weight k + h + 2n. Note that the factor of is included so that the q-expansion coefficients of are rational if those of and are. and 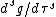are the standard derivatives, as opposed to the derivative with respect to the square of the nome which is sometimes also used.

Representation theory

The mysterious formula for the Rankin–Cohen bracket can be explained in terms of representation theory. Modular forms can be regarded as lowest weight vectors for discrete series representations of SL₂(R) in a space of functions on SL₂(R)/SL₂(Z). The tensor product of two lowest weight representations corresponding to modular forms f and g splits as a direct sum of lowest weight representations indexed by non-negative integers n, and a short calculation shows that the corresponding lowest weight vectors are the Rankin–Cohen brackets [f,g]_n.

References

{{citation|mr=0382192|zbl=0311.10030

|last=Cohen|first= Henri
|title=Sums involving the values at negative integers of L-functions of quadratic characters
|journal=Math. Ann. |volume=217 |year=1975|issue= 3|pages= 271–285|doi=10.1007/BF01436180}}

{{citation|mr=0082563|zbl=0072.08601

|last=Rankin|first= R. A.
|title=The construction of automorphic forms from the derivatives of a given form
|journal=J. Indian Math. Soc. (N.S.)|volume= 20 |year=1956|pages= 103–116}}

{{citation|mr=0092870

|last=Rankin|first= R. A.
|title=The construction of automorphic forms from the derivatives of given forms
|journal=Michigan Math. J. |volume=4 |year=1957|pages= 181–186|doi=10.1307/mmj/1028989013}}

{{citation|mr=1280058|zbl=0806.11022

|last=Zagier|first= Don
|title=Modular forms and differential operators
|series=K. G. Ramanathan memorial issue
|journal=Proc. Indian Acad. Sci. Math. Sci.|volume= 104 |year=1994|issue= 1|pages= 57–75|doi=10.1007/BF02830874}}{{DEFAULTSORT:Rankin-Cohen bracket}}

1 : Modular forms

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。