参数估计canshu guji
通过样本的信息对有关总体参数的情况进行推估。包括点估计和区间估计。
点估计是用样本统计量的一个具体值来估计相应的总体参数。如在一个样本中，可得出一个样本平均数＝60，用它作为总体平均数μ的估计值；当然它不一定刚好等于μ，但希望尽量接近于μ，因此＝60就是μ的点估计。可见点估计是一种不大精确的估计。如果取多个样本统计量的平均值来估计总体参数，则要准确得多；如μ＝μ,μs2＝σ2等。但取多个样本较耗时费力。
区间估计是在一次抽样中以某种样本统计量来估计相应总体参数时，用较大的概率（称为置信度）来保证这种估计。例如在一个容量为36的样本中计得＝56，则它相应的总体参数μ不一定刚好为56，而是在56附近的某个区间内。由于μ是未知的，我们只能以较大的概率(如95%)来保证μ落在56附近的某个区间内。这个区间就称为置信区间。其步骤是：❶确定统计量的抽样分布服从何种分布。如前面已知当n较大时的抽样分布服从于正态分布。
❷确定统计量的标准误。如的标准误为SE＝S/
,n为已知，S可在样本中计出(假定S=10)。
❸确定置信度P或置信水平(小概率a=1—p) 一般p取0.95 (a=0.05)或0.99 (a=0.01)。
❹在统计量所服从的分布中找到a/2与(1—a/2)的界限值，如设a=0.05，则在正态分布表中可查到，Za/2=-1.96,Z(1-σ/2)=1.96。
❺据下面表1的有关公式写出样本统计量的估计相应总体参数的置信区间。本例中可知，X估计μ的置信区间为[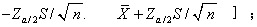
；把上述各数值代入此区间即得[52.08,59.92]。这就是说.我们以95%的把握估计μ落在[52.08,59.92]内；或者说，μ落入[52.08,59.92]的概率为0.95.
表1 一个总体的主要参数估计一览表
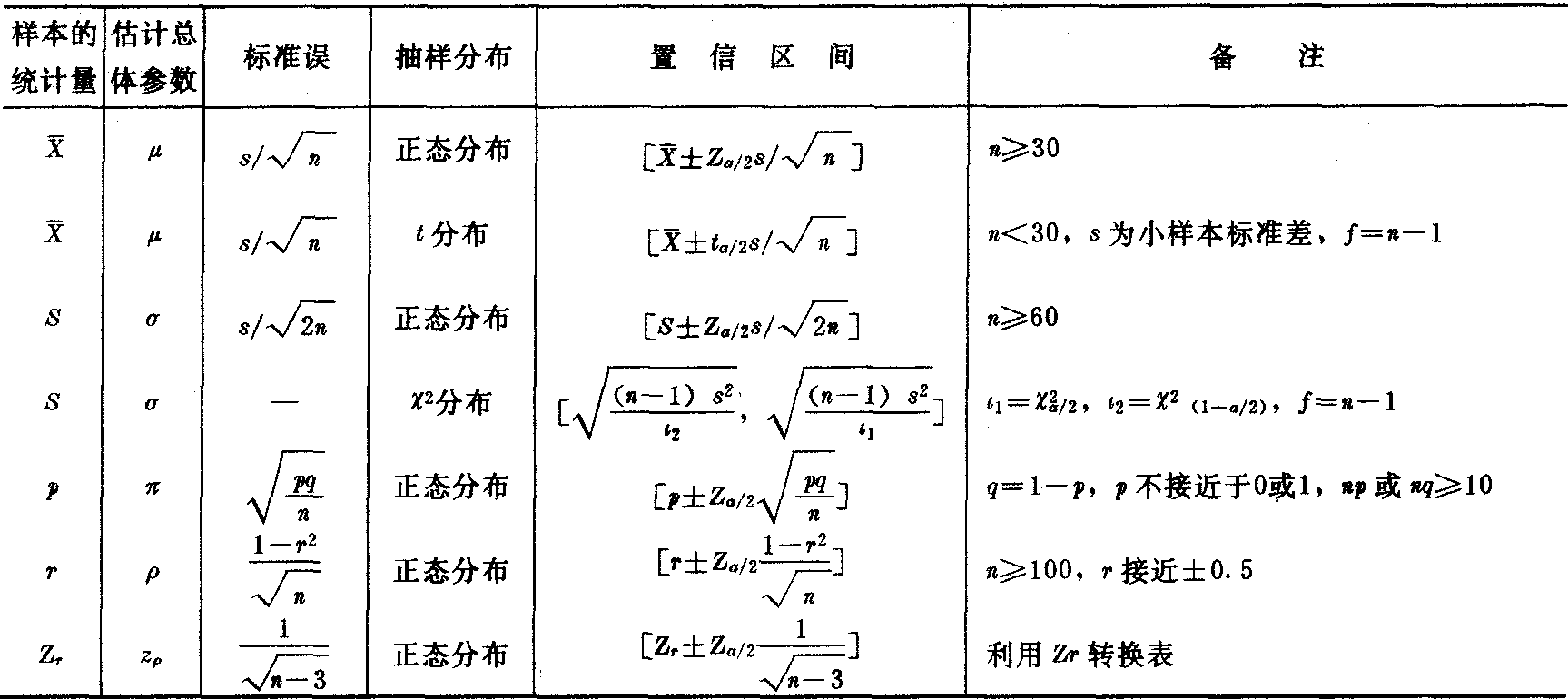
注：p为比例或百分比，r为相关系数，Zr是r对z的转换值。
[例1] 从某市初中毕业生中随机抽取1000名学生，测得他们的近视率为25%。利用表1中关于比例的置信区间公式可求得(设α=0.05)该市初中毕业生总体的近视率为：
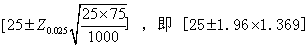
故以95%的把握推断该市初中毕业生总体的近视率在22.3～27.7%之间。
表2 关于二个总体的主要参数估计一览表
[例2] 为调查某市中学生体育锻炼达标情况，随机抽查男生2500人中有1 300人达标，女生1800人中有1 100人达标。试对全市中学男、女生达标率之差异做出估计(取α=0.05)。
在表2中找到关于两总体率π1-π2的置信区间公
即[0.06,0.12]。这就是说，在样本中它们相差0.09，而在总体中它们差异是在0.06～0.12之间，而且是以95%的把握作出这一估计的。参数估计parameter estimation
由总体抽得的样本估计该总体的未知参数的统计推断方法，可分为参数的点估计和区间估计。
参数的点估计 用样本的特征数估计总体相应的特征数，其常用方法有矩估计法和极大似然法两种。
矩估计法 用样本的r阶矩作为总体的r阶矩的估值。设x1,x2，…，xn是容量为n的样本，k为自然数，分别称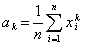
和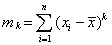
为k阶样本原点矩和k阶样本中心矩，统称为样本矩。设总体X的分布函数为F(x),k为任一正整数，分别称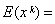
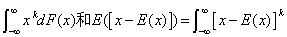dF(x)为总体X的k阶原点矩分别是它的数学期望μ和方差σ2，所以可用一阶样本原点矩
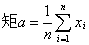和二阶样本中心矩
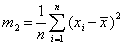分别来估计总体均值μ和方差σ2
极大似然法 设总体X的分布是连续的，其密度
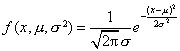
因此，似然函数为
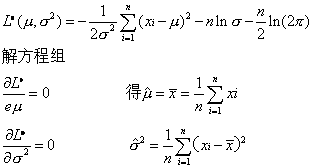
分别为μ与σ2的极大似然估计值。
可用来估计参数θ的估计量很多，因而产生了估计量的优良性问题，这种优良性的标准不是唯一的，可以根据问题的实际背景和应用方便进行选择，主要包括参数估计量的无偏性、有效性和一致性。
如果参数θ的估计量θ满足关系E(θ)=θ，则称θ是θ的无偏估计。
若θ1和θ2都是θ的无偏估计，且两者的方差比
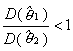
则称θ1比θ2有效。如果固定样本容量n，使D(θ)=极小值的无偏估计值，θ就称为θ的有效估值。
若样本容量n趋向无穷大即n→∞时，θ→θ，则称θ是θ的一致估计量。
参数的区间估计 由总体抽得的样本来估计在一定概率保证下包含总体参数θ的区间[L1、L2]的统计推断方法。保证参数θ在该区间的概率P=1-α(农化研究中α常取0.05和0.01)称为置信概率或置信度。这个区间[L1、L2]称为θ的1-α置信区间，其中L2、L1分别称为置信上限和置信下限，统称为置限。正态总体的均值μ的1-α置信上、下限列于下表，表中
数，可查正态分布和t分布表得到（见抽样分布）。
正态总体均值μ的1-α置信上、下限表
参数估计
数理统计的一个重要内容。见“非参数统计”。
参数估计
由样本(Z1,Z2，…，Zn)对总体分布F(x;θ)中的未知参数θ进行估计的方法。是统计推断的基本问题之一。分为点估计和区间估计两类。在实际工作中，已知或由大量累计资料可以确定研究总体的分布类型，但分布参数未知，或者人们只关心分布中某些数字特征，这就需要由有限样本来估计未知参数，从而掌握总体分布特征。如评价产品的平均质量指标，质量波动程度，两批同类产品的质量对比，同地区某一指标的对比及总体比例(如产品的合格率，返修率，出生率)等方面，有些不能采用普查方法，同时为了省时省力而采用随机抽样方法，用样本资料对其真值进行估计。常被应用于测验分数统计中。