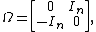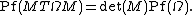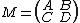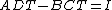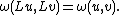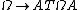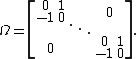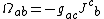- Properties
- Symplectic transformations
- The matrix Ω
- Diagonalisation and decomposition
- Complex matrices
- Applications
- See also
- References
- External links
In mathematics, a symplectic matrix is a {{math|2n × 2n}} matrix M with real entries that satisfies the condition
{{NumBlk|:| |{{EquationRef|1}}}}
|{{EquationRef|1}}}}where MT denotes the transpose of M and Ω is a fixed {{math|2n × 2n}} nonsingular, skew-symmetric matrix. This definition can be extended to {{math|2n × 2n}} matrices with entries in other fields, such as the complex numbers.
Typically Ω is chosen to be the block matrix
where In is the {{math|n × n}} identity matrix. The matrix Ω has determinant +1 and has an inverse given by Ω−1 = ΩT = −Ω.
Every symplectic matrix has determinant 1, and the {{math|2n × 2n}} symplectic matrices with real entries form a subgroup of the special linear group SL(2n, R) under matrix multiplication. Topologically, this symplectic group is a connected noncompact real Lie group of real dimension {{nowrap|n(2n + 1)}}, and is denoted Sp(2n, R). The symplectic group can be defined as the set of linear transformations that preserve the symplectic form of a real symplectic vector space.
Examples of symplectic matrices include the identity matrix and the matrix  .
.
Properties
Every symplectic matrix is invertible with the inverse matrix given by
Furthermore, the product of two symplectic matrices is, again, a symplectic matrix. This gives the set of all symplectic matrices the structure of a group. There exists a natural manifold structure on this group which makes it into a (real or complex) Lie group called the symplectic group.
It follows easily from the definition that the determinant of any symplectic matrix is ±1. Actually, it turns out that the determinant is always +1 for any field. One way to see this is through the use of the Pfaffian and the identity
Since 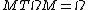 and
and 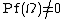 we have that det(M) = 1.
we have that det(M) = 1.
When the underlying field is real or complex, one can also show this by factoring the inequality 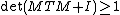 .[1]
.[1]
Suppose Ω is given in the standard form and let M be a 2n×2n block matrix given by
where A, B, C, D are n×n matrices. The condition for M to be symplectic is equivalent to the two following equivalent conditions[2]
symmetric, and
symmetric, and
When n = 1 these conditions reduce to the single condition det(M) = 1. Thus a 2×2 matrix is symplectic iff it has unit determinant.
With Ω in standard form, the inverse of M is given by
The group has dimension n(2n + 1). This can be seen by noting that the group condition implies that
this gives equations of the form
where  is the i,j-th element of M. The sum is antisymmetric with respect to indices i,j, and since the left hand side is zero when i differs from j, this leaves n(2n+1) independent equations.
is the i,j-th element of M. The sum is antisymmetric with respect to indices i,j, and since the left hand side is zero when i differs from j, this leaves n(2n+1) independent equations.
Symplectic transformations
In the abstract formulation of linear algebra, matrices are replaced with linear transformations of finite-dimensional vector spaces. The abstract analog of a symplectic matrix is a symplectic transformation of a symplectic vector space. Briefly, a symplectic vector space is a 2n-dimensional vector space V equipped with a nondegenerate, skew-symmetric bilinear form ω called the symplectic form.
A symplectic transformation is then a linear transformation L : V → V which preserves ω, i.e.
Fixing a basis for V, ω can be written as a matrix Ω and L as a matrix M. The condition that L be a symplectic transformation is precisely the condition that M be a symplectic matrix:
Under a change of basis, represented by a matrix A, we have
One can always bring Ω to either the standard form given in the introduction or the block diagonal form described below by a suitable choice of A.
The matrix Ω
Symplectic matrices are defined relative to a fixed nonsingular, skew-symmetric matrix Ω. As explained in the previous section, Ω can be thought of as the coordinate representation of a nondegenerate skew-symmetric bilinear form. It is a basic result in linear algebra that any two such matrices differ from each other by a change of basis.
The most common alternative to the standard Ω given above is the block diagonal form
This choice differs from the previous one by a permutation of basis vectors.
Sometimes the notation J is used instead of Ω for the skew-symmetric matrix. This is a particularly unfortunate choice as it leads to confusion with the notion of a complex structure, which often has the same coordinate expression as Ω but represents a very different structure. A complex structure J is the coordinate representation of a linear transformation that squares to −1, whereas Ω is the coordinate representation of a nondegenerate skew-symmetric bilinear form. One could easily choose bases in which J is not skew-symmetric or Ω does not square to −1.
Given a hermitian structure on a vector space, J and Ω are related via
where 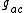 is the metric. That J and Ω usually have the same coordinate expression (up to an overall sign) is simply a consequence of the fact that the metric g is usually the identity matrix.
is the metric. That J and Ω usually have the same coordinate expression (up to an overall sign) is simply a consequence of the fact that the metric g is usually the identity matrix.
Diagonalisation and decomposition
- For any positive definite real symplectic matrix {{math|S}} there exists {{math|U}} in {{math|U(2n,R)}} such that
where the diagonal elements of {{math|D}} are the eigenvalues of {{math|S}}.[3]
- Any real symplectic matrix {{math|S}} has a polar decomposition of the form:[3]
- Any real symplectic matrix can be decomposed as a product of three matrices:
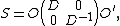
|{{EquationRef|2}}}} such that {{math|O}} and {{math|O'}} are both symplectic and orthogonal and {{math|D}} is positive-definite and diagonal.[4] This decomposition is closely related to the singular value decomposition of a matrix and is known as an 'Euler' or 'Bloch-Messiah' decomposition.
Complex matrices
If instead M is a 2n×2n matrix with complex entries, the definition is not standard throughout the literature. Many authors [5] adjust the definition above to
{{NumBlk|:| |{{EquationRef|3}}}}
|{{EquationRef|3}}}}where M* denotes the conjugate transpose of M. In this case, the determinant may not be 1, but will have absolute value 1. In the 2×2 case (n=1), M will be the product of a real symplectic matrix and a complex number of absolute value 1.
Other authors [6] retain the definition ({{EquationNote|1}}) for complex matrices and call matrices satisfying ({{EquationNote|3}}) conjugate symplectic.
Applications
Transformations described by symplectic matrices play an important role in quantum optics and in continuous-variable quantum information theory. For instance, symplectic matrices can be used to describe Gaussian (Bogoliubov) transformations of a quantum state of light.[7] In turn, the Bloch-Messiah decomposition ({{EquationNote|2}}) means that such an arbitrary Gaussian transformation can be represented as a set of two passive linear-optical interferometers (corresponding to orthogonal matrices O and O' ) intermitted by a layer of active non-linear squeezing transformations (given in terms of the matrix D).[8] In fact, one can circumvent the need for such in-line active squeezing transformations if two-mode squeezed vacuum states are available as a prior resource only.[9]
See also
{{Portal|Mathematics}}- symplectic vector space
- symplectic group
- symplectic representation
- orthogonal matrix
- unitary matrix
- Hamiltonian mechanics
- Linear complex structure
References
2. ^{{cite web|last1=de Gosson|first1=Maurice|title=Introduction to Symplectic Mechanics: Lectures I-II-III|url=https://www.ime.usp.br/~piccione/Downloads/LecturesIME.pdf}}
3. ^1 {{Cite book|title=Symplectic Methods in Harmonic Analysis and in Mathematical Physics - Springer|last=de Gosson|first=Maurice A.|language=en|doi=10.1007/978-3-7643-9992-4|year = 2011|isbn = 978-3-7643-9991-7}}
4. ^{{harvnb|Ferraro et. al.|2005}} Section 1.3. ... Title?
5. ^{{cite journal|last = Xu|first= H. G.|title= An SVD-like matrix decomposition and its applications|journal= Linear Algebra and its Applications|date= July 15, 2003|volume= 368|pages=1–24|doi = 10.1016/S0024-3795(03)00370-7}}
6. ^{{Cite journal|last1=Mackey |last2= Mackey|first1= D. S. |first2= N.|title= On the Determinant of Symplectic Matrices|year= 2003|series=Numerical Analysis Report| volume= 422|publisher=Manchester Centre for Computational Mathematics|location=Manchester, England}}
7. ^{{Cite journal|last=Weedbrook|first=Christian|last2=Pirandola|first2=Stefano|last3=García-Patrón|first3=Raúl|last4=Cerf|first4=Nicolas J.|last5=Ralph|first5=Timothy C.|last6=Shapiro|first6=Jeffrey H.|last7=Lloyd|first7=Seth|date=2012|title=Gaussian quantum information|journal=Reviews of Modern Physics|volume=84|issue=2|pages=621–669|arxiv=1110.3234|doi=10.1103/RevModPhys.84.621}}
8. ^{{Cite journal|last=Braunstein|first=Samuel L.|title=Squeezing as an irreducible resource|date=2005|journal=Physical Review A|volume=71|pages=055801|doi=10.1103/PhysRevA.71.055801|arxiv=quant-ph/9904002}}
9. ^{{cite journal|last1=Chakhmakhchyan|first1=Levon|last2=Cerf|first2=Nicolas|title= Simulating arbitrary Gaussian circuits with linear optics|journal=Physical Review A|date=2018|volume=98|page=062314|doi=10.1103/PhysRevA.98.062314|arxiv=1803.11534}}
External links
- {{planetmath reference|id=4140|title=Symplectic matrix}}
- {{planetmath reference|id=7455|title=The characteristic polynomial of a symplectic matrix is a reciprocal polynomial}}
- Georgy Gurtskaia
- Georgy Gurtskaya
- Georgy I. Andryushchenko
- Georgy II
- Georgy II Vsevolodovich
- Georgy Kabulov
- Georgy Karyukhin
- Georgy Kechaari
- Georgy Ketoev
- Georgy Ketoyev
- Georgy Klimov
- Georgy Kolpakov
- Georgy Kondratiev
- Georgy Kondratyev
- Georgy Kornienko
- Georgy Koshlakov
- Georgy Kudryavtsev
- Georgy Kulov
- Georgy Lisitsin
- Georgy Lisitsyn
- Georgy Lukacs
- Georgy Mamedov
- Georgy Martynovitch Kert
- Georgy Matsievsky
- Georgy Matveev