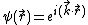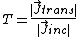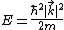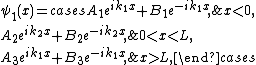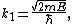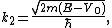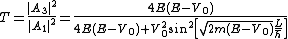“Resonances in scattering from potentials”的意思、由来-开放百科全书

词条

Resonances in scattering from potentials

释义

One Dimensional Case : Finite Square Potential
Mathematical Description The Physical Picture: Standing de Broglie Waves and the Fabry-Pérot Etalon Nature Of Resonance Curves
References

In quantum mechanics, resonance occurs in the context of scattering theory, which deals with studying scattering of quantum particles from potentials. The scattering problem deals with calculation of flux distribution of scattered particles/waves as a function of the potential, and of the state (characterized by momentum/energy) of the incident particle. For a free quantum particle incident on the potential, the plane wave solution to the time independent Schrödinger equation is :

For one dimensional problems, we are interested in the transmission coefficient 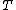, defined as :

where is the probability current density. This gives the fraction of incident beam of particles that makes it through the potential. For three dimensional problems, we calculate the scattering cross-section , which, roughly speaking, is the total area of the incident beam which is scattered. Another quantity of relevance is the partial cross-section, 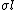, which denotes the scattering cross section for a partial wave of a definite angular momentum eigenstate. These quantities naturally depend on 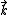, the wave-vector of the incident wave, which is related to its energy by:

The values of these quantities of interest, the transmission coefficient 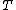(in case of one dimensional potentials), and the partial cross-section 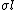show peaks in their variation with the incident energy E. These phenomena are called resonances.

One Dimensional Case : Finite Square Potential

Mathematical Description

A one dimensional finite square potential is given by

The sign of determines whether the square potential is a well or a barrier. To study the phenomena of resonance, we solve for a stationary state with energy 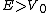The solution to the time independent Schrödinger equation:

for the three regions 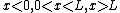are

and are the wave numbers in the potential free region and within the potential respectively,

To calculate 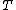, we set 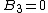to correspond to the fact that there is no wave incident on the potential from the right.Imposing the condition that the wave function 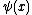, and its derivative 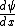should be continuous at and 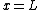, we find relations between the coefficients, which allows us to find 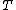as

We see that, the Transmission co-efficient 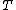reaches its maximum value of 1, when :

.

This is the resonance condition, which leads to the peaking of 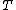to its maxima, called resonance.

The Physical Picture: Standing de Broglie Waves and the Fabry-Pérot Etalon

From the above expression, resonance occurs when the distance covered by the particle in traversing the well and back () is an integral multiple of the De Broglie wavelength of particle inside the potential (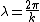). For 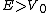, reflections at potential discontinuities are not accompanied by any phase change.^[1] Therefore, resonances correspond to formation of standing waves within the potential barrier/well. At resonance, the waves incident on the potential at and the waves reflecting between the walls of the potential are in phase, and reinforce each other. Far from resonances, standing waves can't be formed. Then, waves reflecting between both walls of the potential( at and 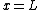) and the wave transmitted through are out of phase, and destroy each other by interference. The physics is similar to that of transmission in Fabry–Pérot interferometer in optics, where the resonance condition and functional form of Transmission co-efficient are the same.

Nature Of Resonance Curves

As a function of the length of square well (), the Transmission coefficient swings between its maximum of 1 and minimum of 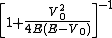, with a period of 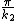. As a function of energy, the first term in the denominator dominates the oscillating term for 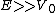and therefore, . Sharper resonances occur at lower energies,where the oscillating term in the denominator controls the behaviour of 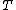. The resonances become flat at higher energies, because the minimas of 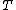get higher with as the effect of the oscillatory term in the denominator diminishes. This is demonstrated in plots of Transmission coefficient against incident particle energy for fixed values of the shape factor, defined as

1. ^Claude Cohen-Tannaoudji, Bernanrd Diu,Frank Laloe.(1992),Quantum Mechanics( Vol. 1),Wiley-VCH, p.73

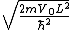
References

{{cite book | author=Merzbacher Eugene | title=Quantum Mechanics | publisher=John Wiley and Sons }}
{{cite book | author=Cohen-Tannoudji Claude | title=Quantum Mechanics | publisher=Wiley-VCH }}

1 : Quantum mechanics

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。