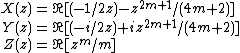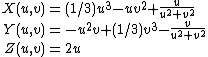- References
In differential geometry, a Richmond surface is a minimal surface first described by Herbert William Richmond in 1904. [1] It is a family of surfaces with one planar end and one Enneper surface-like self-intersecting end.
It has Weierstrass–Enneper parameterization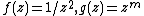 
. This allows a parametrization based on a complex parameter as
The associate family of the surface is just the surface rotated around the z-axis.
Taking m = 2 a real parametric expression becomes:[2]
References
1. ^ Jesse Douglas, Tibor Radó, The Problem of Plateau: A Tribute to Jesse Douglas & Tibor Radó, World Scientific, 1992 (p. 239-240)
2. ^John Oprea, The Mathematics of Soap Films: Explorations With Maple, American Mathematical Soc., 2000
{{Minimal surfaces}}2. ^John Oprea, The Mathematics of Soap Films: Explorations With Maple, American Mathematical Soc., 2000
1 : Minimal surfaces
- South Devon and Tavistock Railway
- South Devon Area of Outstanding Natural Beauty
- South Devon Banks
- South Devon (disambiguation)
- South Devon Football League
- South Devon League
- South Devon Railway 0-4-0 locomotives
- South Devon Railway 0-4-0 locomotives Owl class
- South Devon Railway 0-4-0 Owl class steam locomotive
- South Devon Railway (1846-1876)
- South Devon Railway 2-4-0 locomotives
- South Devon Railway Buffalo class
- South Devon Railway Comet class
- South Devon Railway Company
- South Devon Railway Dido class
- South Devon Railway Eagle class
- South Devon Railway engine houses
- South Devon Railway Gorgon class
- South Devon Railway Leopard class
- South Devon Railway locomotives
- South Devon Railway locomotive Taurus
- South Devon Railway Remus class
- South Devon Railway sea wall
- South Devon Railway Tornado class
- South Devon (UK Parliament constituency)