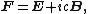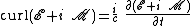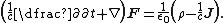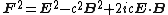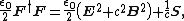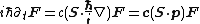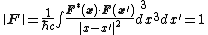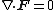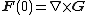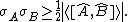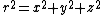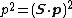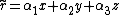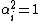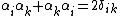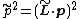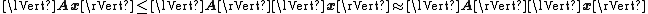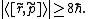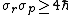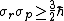请输入您要查询的百科知识：

　

词条 Riemann–Silberstein vector
释义

  1. Definition

  2. Application

  3. Photon wave function

     Schrödinger equation for the photon and the Heisenberg uncertainty relations 

  4. References

{{electromagnetism}}

In mathematical physics, in particular electromagnetism, the Riemann–Silberstein vector, named after Bernhard Riemann and Ludwik Silberstein, (or sometimes ambiguously called the "electromagnetic field") is a complex vector that combines the electric field E and the magnetic field B.[1][2]

Definition

Given an electric field E and a magnetic field B defined on a common region of spacetime, the Riemann–Silberstein vector is

where c is the speed of light, with some authors preferring to multiply the right hand side by an overall constant 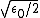, where ε0 is the permittivity of free space. It is analogous to the electromagnetic tensor F, a 2-vector used in the covariant formulation of classical electromagnetism.

In Silberstein's formulation, i was defined as the imaginary unit, and F was defined as a complexified 3-dimensional vector field, called a bivector field.[3]

Application

{{main article|Maxwell's equations}}

Bernhard Riemann used 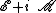to illustrate consolidation of Maxwell’s equations. According to lectures published by Heinrich Martin Weber in 1901, the real and imaginary components of the equation

are an interpretation of Maxwell’s equations without charges or currents. Riemann’s lectures are available on-line from University of Michigan Historical Math Collection in Weber’s book, §138, S. 348, under the title Zusammenziehung der Maxwell’schen Gleichungen (Consolidation of Maxwell’s Equations).[4]

The Riemann–Silberstein vector is used as a point of reference in the geometric algebra formulation of electromagnetism. Maxwell's four equations in vector calculus reduce to one equation in the algebra of physical space:

Expressions for the fundamental invariants and the energy density and momentum density also take on simple forms:

where S is the Poynting vector.

The Riemann–Silberstein vector is used for an exact matrix representations of Maxwell's equations in an inhomogeneous medium with sources.[5][6]

Photon wave function

In 1996 contribution to quantum electrodynamics, Iwo Bialynicki-Birula used the Riemann–Silberstein vector as the basis for an approach to the photon, noting that it is a "complex vector-function of space coordinates r and time t that adequately describes the quantum state of a single photon". To put the Riemann–Silberstein vector in contemporary parlance, a transition is made:

With the advent of spinor calculus that superseded the quaternionic calculus, the transformation properties of the Riemann-Silberstein vector have become even more transparent ... a symmetric second-rank spinor.

Bialynicki-Birula acknowledges that the photon wave function is a controversial concept and that it cannot have all the properties of Schrödinger wave functions of non-relativistic wave mechanics. Yet defense is mounted on the basis of practicality: it is useful for describing quantum states of excitation of a free field, electromagnetic fields acting on a medium, vacuum excitation of virtual positron-electron pairs, and presenting the photon among quantum particles that do have wave functions.

Schrödinger equation for the photon and the Heisenberg uncertainty relations

Multiplying the two time dependent Maxwell equations by

the Schrödinger equation for photon in the vacuum is given by

where 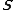is the vector built from the spin of the length 1 matrices generating full infinitesimal rotations of 3-spinor particle. One may therefore notice that the

Hamiltonian in the Schrödinger equation of the photon is the projection of its spin 1 onto

its momentum since the normal momentum operator appears there from combining parts of rotations.

In contrast to the electron wave function the modulus square of the wave function of the photon

(Riemann-Silbertein vector) is not dimensionless and must be multiplied by the "local photon

wavelength" with the proper power to give dimensionless expression to normalize i.e.

it is normalized in the exotic way with the integral kernel

The two residual Maxwell equations are only constraints i.e.

and they are automatically fulfilled all time if only fulfilled at the initial time

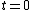, i.e.

where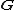

is any complex vector field with the non-vanishing rotation, or

it is a vector potential for the Riemann–Silberstein vector.

While having the wave function of the photon one can estimate the uncertainty relations

for the photon.[7] It shows up that photons are "more quantum" than the electron while their

uncertainties of position and the momentum are higher. The natural candidates to estimate the uncertainty are the natural momentum like simply the projection 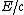or 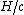from Einstein

formula for the photoelectric effect and the simplest theory of quanta and the , the uncertainty

of the position length vector.

We will use the general relation for the uncertainty for the operators

We want the uncertainty relation for 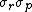i.e. for the operators

The first step is to find the auxiliary operator such that this relation

can be used directly. First we make the same trick for that Dirac made to calculate the

square root of the Klein-Gordon operator to get the Dirac equation:

where are matrices from the Dirac equation:

Therefore, we have

Because the spin matrices 1 are only to calculate the commutator

in the same space we approximate the spin matrices

by angular momentum matrices of the particle with the length 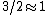while

dropping the multiplying 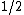since the resulting Maxwell equations in 4 dimensions would look too artificial

to the original (alternatively we can keep the original 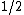factors but normalize the new 4-spinor

to 2 as 4 scalar particles normalized to 1/2):

We can now readily calculate the commutator while calculating commutators

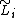of matrixes and scaled and noticing that the symmetric Gaussian state

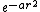is annihilating in average the terms containing mixed variable like

Calculating 9 commutators (mixed may be zero by Gaussian example and the 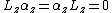since those matrices are counter-diagonal) and estimating

terms from the norm of the resulting 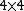matrix containing four 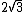factors giving square of the most natural 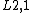norm of this matrix as 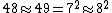and using the norm inequality for the estimate

we obtain

or

which is much more than for the mass particle in 3 dimensions that is

and therefore photons turn out to be particles

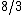times or almost 3 times "more quantum" than particles with the mass like electrons.

References

1. ^{{Cite journal |last=Silberstein |first=Ludwik |year=1907 |title=Elektromagnetische Grundgleichungen in bivectorieller Behandlung |url=http://neo-classical-physics.info/uploads/3/0/6/5/3065888/silberstein_-_em_equations_in_bivector_fomr.pdf |journal=Annalen der Physik |volume=327 |issue= 3|pages=579–586 |bibcode=1907AnP...327..579S |doi=10.1002/andp.19073270313}}
2. ^{{Cite journal |last=Silberstein |first=Ludwik |year=1907 |title=Nachtrag zur Abhandlung über 'Elektromagnetische Grundgleichungen in bivectorieller Behandlung' |url=http://neo-classical-physics.info/uploads/3/0/6/5/3065888/silberstein_-_addendum.pdf |journal=Annalen der Physik |volume=329 |pages=783–784 |bibcode=1907AnP...329..783S |doi=10.1002/andp.19073291409 |issue=14}}
3. ^{{cite journal |last=Aste |first=Andreas |year=2012 |title=Complex representation theory of the electromagnetic field |journal=Journal of Geometry and Symmetry in Physics |volume=28 |pages=47–58 |doi=10.7546/jgsp-28-2012-47-58|arxiv = 1211.1218 }}
4. ^Heinrich Martin Weber (1901) Die partiellen Differential-Gleichungen der mathematischen Physik nach Riemann's Vorlesungen, Zweiter Band S. 348, Braunscheweig: Friedrich Vieweg und Sohn, available from [ University of Michigan Historical Math Collection]
5. ^{{cite journal |last=Bialynicki-Birula |first=Iwo |year=1996 |title=Photon wave function |journal=Progress in Optics |volume=36 |issue= |pages=245–294 |arxiv=quant-ph/0508202 |bibcode= |doi=10.1016/S0079-6638(08)70316-0 |series= |isbn=978-0-444-82530-8}}
6. ^{{cite journal |last1=Khan |first1=Sameen Ahmed |year=2005 |title=An Exact Matrix Representation of Maxwell's Equations |journal=Physica Scripta |volume=71 |issue=5 |pages=440 |arxiv=physics/0205083 |bibcode=2005PhyS...71..440K |doi=10.1238/Physica.Regular.071a00440}}
7. ^{{cite journal|url=http://www.cft.edu.pl/~birula/publ/PhotUncert.pdf|doi=10.1103/physrevlett.108.140401|title=Uncertainty Relation for Photon|author=Bialynicki-Birula, Iwo|author2=|journal=Phys. Rev. Lett.|volume=108|pages=140401-1-5|issue=|year = 2012|arxiv = 1110.2415 |bibcode = 2012PhRvL.108n0401B }}- This publication is using slightly different definitions of position and momentum uncertainties resigning from the position operator and normalizing uncertainty of to uncertainty of r
{{DEFAULTSORT:Riemann-Silberstein vector}}

3 : Electromagnetism|Geometric algebra|Bernhard Riemann
随便看

　

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

　

Copyright © 2023 OENC.NET All Rights Reserved
京ICP备2021023879号 更新时间：2024/11/12 11:20:22