“Tamagawa number”的意思、由来-开放百科全书

词条

Tamagawa number

释义

Definition
Weil's conjecture on Tamagawa numbers
See also
References
Further reading

In mathematics, the Tamagawa number 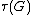of a semisimple algebraic group defined over a global field {{math|k}} is the measure of 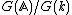, where is the adele ring of {{math|k}}. Tamagawa numbers were introduced by {{harvs|txt|authorlink=Tsuneo Tamagawa|last=Tamagawa|year=1966}}, and named after him by {{harvs|txt|authorlink=André Weil|last=Weil|year=1959}}.

Tsuneo Tamagawa's observation was that, starting from an invariant differential form ω on {{math|G}}, defined over {{math|k}}, the measure involved was well-defined: while {{math|ω}} could be replaced by {{math|cω}} with {{math|c}} a non-zero element of , the product formula for valuations in {{math|k}} is reflected by the independence from {{math|c}} of the measure of the quotient, for the product measure constructed from {{math|ω}} on each effective factor. The computation of Tamagawa numbers for semisimple groups contains important parts of classical quadratic form theory.

Definition

Let {{math|k}} be a global field, {{math|A}} its ring of adeles, and {{math|G}} a semisimple algebraic group defined over {{math|k}}.

Choose Haar measures on the completions {{math|k_v of k}} such that {{math|O_v}} has volume 1 for all but finitely many places {{math|v}}. These then induce a Haar measure on {{math|A}}, which we further assume is normalized so that {{math|A/k}} has volume 1 with respect to the induced quotient measure.

The Tamagawa measure on the adelic algebraic group {{math|G(A)}} is now defined as follows. Take a left-invariant {{math|n}}-form {{math|ω}} on {{math|G(k)}} defined over {{math|k}}, where {{math|n}} is the dimension of {{math|G}}. This, together with the above choices of Haar measure on the {{math|k_v}}, induces Haar measures on {{math|G(k_v)}} for all places of {{math|v}}. As {{math|G}} is semisimple, the product of these measures yields a Haar measure on {{math|G(A)}}, called the Tamagawa measure. The Tamagawa measure does not depend on the choice of ω, nor on the choice of measures on the {{math|k_v}}, because multiplying {{math|ω}} by an element of {{math|k*}} multiplies the Haar measure on {{math|G(A)}} by 1, using the product formula for valuations.

The Tamagawa number {{math|τ(G)}} is defined to be the Tamagawa measure of {{math|G(A)/G(k)}}.

Weil's conjecture on Tamagawa numbers

Weil's conjecture on Tamagawa numbers states that the Tamagawa number {{math|τ(G)}} of a simply connected (i.e. not having a proper algebraic covering) simple algebraic group defined over a number field is 1. {{harvs|txt|authorlink=André Weil|last=Weil|year=1959}} calculated the Tamagawa number in many cases of classical groups and observed that it is an integer in all considered cases and that it was equal to 1 in the cases when the group is simply connected. {{harvtxt|Ono|1963}} found examples where the Tamagawa numbers are not integers, but the conjecture about the Tamagawa number of simply connected groups was proven in general by several works culminating in a paper by {{harvs|txt|authorlink=Robert Kottwitz|last=Kottwitz|year=1988}} and for the analogue over function fields over finite fields by Lurie and Gaitsgory in 2011.{{sfn|Lurie|2014}}

References

{{Springer|id=T/t092060|title=Tamagawa number}}
{{citation|last= Kottwitz|first= Robert E. |title=Tamagawa numbers |journal= Ann. of Math. |series= 2 |volume= 127 |year=1988|issue= 3|pages=629–646|doi=10.2307/2007007|jstor=2007007|publisher=Annals of Mathematics|mr= 0942522}}.
{{Citation | last1=Ono | first1=Takashi | authorlink=Takashi Ono (mathematician) | title=On the Tamagawa number of algebraic tori | jstor=1970502 |mr=0156851 | year=1963 | journal=Annals of Mathematics |series=Second Series | issn=0003-486X | volume=78 | pages=47–73 | doi=10.2307/1970502}}
{{Citation | last1=Ono | first1=Takashi | title=On the relative theory of Tamagawa numbers | jstor=1970563 |mr=0177991 | year=1965 | journal=Annals of Mathematics |series=Second Series | issn=0003-486X | volume=82 | pages=88–111 | doi=10.2307/1970563}}
{{Citation | last1=Tamagawa | first1=Tsuneo | title=Algebraic Groups and Discontinuous Subgroups | publisher=American Mathematical Society | location=Providence, R.I. | series=Proc. Sympos. Pure Math. |mr=0212025 | year=1966 | volume=IX | chapter=Adèles | pages=113–121}}
{{Citation | last1=Weil | first1=André | author1-link=André Weil | title=Exp. No. 186, Adèles et groupes algébriques | url=http://www.numdam.org/item?id=SB_1958-1960__5__249_0 | series=Séminaire Bourbaki | year=1959 | volume=5 | pages=249–257}}
{{Citation | last1=Weil | first1=André | author1-link=André Weil | title=Adeles and algebraic groups | origyear=1961 | url=https://books.google.com/books/about/Adeles_and_algebraic_groups.html?id=vQvvAAAAMAAJ | publisher=Birkhäuser Boston | location=Boston, MA | series=Progress in Mathematics | isbn=978-3-7643-3092-7 |mr=670072 | year=1982 | volume=23}}
{{Citation | last=Lurie | first=Jacob | author-link=Jacob Lurie | title=Tamagawa Numbers via Nonabelian Poincaré Duality | year=2014 | url=http://www.math.harvard.edu/~lurie/282y.html }}

Definition

Weil's conjecture on Tamagawa numbers

See also

References

Further reading