- Algorithms Non-convex method Convex relaxation
- Applications Video surveillance Face recognition
- Surveys
- Books, journals and workshops Books Journals Workshops Sessions
- Resources and libraries Websites Libraries
- References
- External links
Robust Principal Component Analysis (RPCA) is a modification of the widely used statistical procedure of principal component analysis (PCA) which works well with respect to grossly corrupted observations. A number of different approaches exist for Robust PCA, including an idealized version of Robust PCA, which aims to recover a low-rank matrix L0 from highly corrupted measurements M = L0 +S0.[1] This decomposition in low-rank and sparse matrices can be achieved by techniques such as Principal Component Pursuit method (PCP),[1] Stable PCP,[1] Quantized PCP,[2] Block based PCP,[3] and Local PCP.[4] Then, optimization methods are used such as the Augmented Lagrange Multiplier Method (ALM[5]), Alternating Direction Method (ADM[6]), Fast Alternating Minimization (FAM[7])
or Iteratively Reweighted Least Squares (IRLS [8][9][10]).
Algorithms
Non-convex method
The state-of-the-art guaranteed algorithm for the robust PCA problem (with the input matrix being 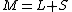 ) is an alternating minimization type algorithm.[11] The computational complexity is
) is an alternating minimization type algorithm.[11] The computational complexity is  where the input is the superposition of a low-rank (of rank
where the input is the superposition of a low-rank (of rank  ) and a sparse matrix of dimension
) and a sparse matrix of dimension  and
and  is the desired accuracy of the recovered solution, i.e.,
is the desired accuracy of the recovered solution, i.e., 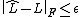 where
where  is the true low-rank component and
is the true low-rank component and 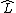 is the estimated or recovered low-rank component. Intuitively, this algorithm performs projections of the residual on to the set of low-rank matrices (via the SVD operation) and sparse matrices (via entry-wise hard thresholding) in an alternating manner - that is, low-rank projection of the difference the input matrix and the sparse matrix obtained at a given iteration followed by sparse projection of the difference of the input matrix and the low-rank matrix obtained in the previous step, and iterating the two steps until convergence.
is the estimated or recovered low-rank component. Intuitively, this algorithm performs projections of the residual on to the set of low-rank matrices (via the SVD operation) and sparse matrices (via entry-wise hard thresholding) in an alternating manner - that is, low-rank projection of the difference the input matrix and the sparse matrix obtained at a given iteration followed by sparse projection of the difference of the input matrix and the low-rank matrix obtained in the previous step, and iterating the two steps until convergence.
Convex relaxation
This method consists of relaxing the rank constraint 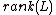 in the optimization problem to the nuclear norm
in the optimization problem to the nuclear norm 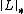 and the sparsity constraint
and the sparsity constraint 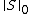 to
to  -norm
-norm 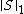 . The resulting program can be solved using methods such as the method of Augmented Lagrange Multipliers.
. The resulting program can be solved using methods such as the method of Augmented Lagrange Multipliers.
Applications
RPCA has many real life important applications particularly when the data under study can naturally be modeled as a low-rank plus a sparse contribution. Following examples are inspired by contemporary challenges in computer science, and depending on the applications, either the low-rank component or the sparse component could be the object of interest:
Video surveillance
Given a sequence of surveillance video frames, it is often required to identify the activities that stand out from the background. If we stack the video frames as columns of a matrix M, then the low-rank component L0 naturally corresponds to the stationary background and the sparse component S0 captures the moving objects in the foreground.[12][13]
Face recognition
Images of a convex, Lambertian surface under varying illuminations span a low-dimensional subspace.[14] This is one of the reasons for effectiveness of low-dimensional models for imagery data. In particular, it is easy to approximate images of a human's face by a low-dimensional subspace. To be able to correctly retrieve this subspace is crucial in many applications such as face recognition and alignment. It turns out that RPCA can be applied successfully to this problem to exactly recover the face.[12]
Surveys
- Robust PCA [13]
- Dynamic RPCA [15]
- Decomposition into Low-rank plus Additive Matrices [16]
- Low-rank models[17]
Books, journals and workshops
Books
- T. Bouwmans, N. Aybat, and E. Zahzah. Handbook on Robust Low-Rank and Sparse Matrix Decomposition: Applications in Image and Video Processing, CRC Press, Taylor and Francis Group, May 2016. (more information: http://www.crcpress.com/product/isbn/9781498724623)
- Z. Lin, H. Zhang, "Low-Rank Models in Visual Analysis: Theories, Algorithms, and Applications", Academic Press, Elsevier, June 2017. (more information: https://www.elsevier.com/books/low-rank-models-in-visual-analysis/lin/978-0-12-812731-5)
Journals
- N. Vaswani, Y. Chi, T. Bouwmans, Special Issue on “Rethinking PCA for Modern Datasets: Theory, Algorithms, and Applications”, Proceedings of the IEEE, 2018.
- T. Bouwmans, N. Vaswani, P. Rodriguez, R. Vidal, Z. Lin, Special Issue on “[https://signalprocessingsociety.org/blog/ieee-jstsp-special-issue-data-science-robust-subspace-learning-and-tracking-theory-algorithms Robust Subspace Learning and Tracking: Theory, Algorithms, and Applications]”, IEEE Journal of Selected Topics in Signal Processing, December 2018.
Workshops
- RSL-CV 2015: Workshop on Robust Subspace Learning and Computer Vision in conjunction with ICCV 2015 (For more information: http://rsl-cv2015.univ-lr.fr/workshop/)
- RSL-CV 2017: Workshop on Robust Subspace Learning and Computer Vision in conjunction with ICCV 2017 (For more information: http://rsl-cv.univ-lr.fr/2017/)
Sessions
- Special Session on "Online Algorithms for Static and Dynamic Robust PCA and Compressive Sensing" in conjunction with SSP 2018. (More information: https://ssp2018.org/)
Resources and libraries
Websites
- Background Subtraction Website
- [https://sites.google.com/site/robustdlam/ DLAM Website]
- Documentation from the University of Illinois
Libraries
LRS Library (A. Sobral, L3i, Univ. La Rochelle, France), The LRSLibrary provides a collection of low-rank and sparse decomposition algorithms in MATLAB. The library was designed for motion segmentation in videos, but it can be also used or adapted for other computer vision. Currently the LRSLibrary contains a total of 72 matrix-based and tensor-based algorithms. The LRSLibrary was tested successfully in MATLAB R2013b both x86 and x64 versions.
References
2. ^{{cite journal|last= S. Becker|author2=E. Candes, M. Grant|title=TFOCS: Flexible First-order Methods for Rank Minimization|journal=Low-rank Matrix Optimization Symposium, SIAM Conference on Optimization|year=2011}}
3. ^{{cite journal|last= G. Tang|author2= A. Nehorai|title=Robust principal component analysis based on low-rank and block-sparse matrix decomposition|journal=Annual Conference on Information Sciences and Systems, CISS 2011|year=2011}}
4. ^{{cite journal|last= B. Wohlberg|author2= R. Chartrand|author3=J. Theiler|title=Local Principal Component Pursuit for Nonlinear Datasets|journal=International Conference on Acoustics, Speech, and Signal Processing, ICASSP 2012|year=2012}}
5. ^{{cite journal|last=Z. Lin|author2= M. Chen|author3=L. Wu|author4=Y. Ma|title=The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices|journal= Journal of Structural Biology|volume= 181|issue= 2|pages= 116–27|arxiv= 1009.5055|doi= 10.1016/j.jsb.2012.10.010|pmid= 23110852|year= 2013|pmc=3565063}}
6. ^{{cite journal|last=X. Yuan|author2= J. Yang|title=Sparse and Low-Rank Matrix Decomposition via Alternating Direction Methods|journal=Optimization Online|year=2009}}
7. ^{{cite journal|last=P. Rodríguez|author2= B. Wohlberg|title=Fast Principal Component Pursuit Via Alternating Minimization|journal=IEEE International Conference on Image Processing, ICIP 2013|year=2013}}
8. ^{{cite journal|last=C. Guyon|author2= T. Bouwmans|author3=E. Zahzah|title=Foreground Detection via Robust Low Rank Matrix Decomposition including Spatio-Temporal Constraint|journal=International Workshop on Background Model Challenges, ACCV 2012|year=2012}}
9. ^{{cite journal|last=C. Guyon|author2= T. Bouwmans|author3=E. Zahzah|title=Foreground Detection via Robust Low Rank Matrix Factorization including Spatial Constraint with Iterative Reweighted Regression|journal=International Conference on Pattern Recognition, ICPR 2012|year=2012}}
10. ^{{cite journal|last=C. Guyon|author2= T. Bouwmans|author3=E. Zahzah|title=Moving Object Detection via Robust Low Rank Matrix Decomposition with IRLS scheme|journal=International Symposium on Visual Computing, ISVC 2012|year=2012}}
11. ^{{cite journal|first1=Netrapalli|last1=P. |first2=Niranjan|last2=U.|first3=Sanghavi|last3=S.|first4=Anandkumar|last4=A.|first5=Jain|last5=P.|title=Non-convex robust PCA|journal=Advances in Neural Information Processing Systems|volume=1410|pages=1107–1115|year=2014|bibcode=2014arXiv1410.7660N|arxiv=1410.7660}}
12. ^1 2 3 {{cite journal|last=Emmanuel J. Candes|author2=Xiaodong Li |author3=Yi Ma |author4=John Wright |title=Robust Principal Component Analysis?}}
13. ^1 {{cite journal|last=T. Bouwmans|author2= E. Zahzah|title=Robust PCA via Principal Component Pursuit: A Review for a Comparative Evaluation in Video Surveillance|journal=Special Issue on Background Models Challenge, Computer Vision and Image Understanding|year=2014}}
14. ^{{cite journal|last=R. Basri|author2=D. Jacobs |title=Lambertian reflectance and linear subspaces}}
15. ^{{cite journal|last=N. Vaswani|author2= T. Bouwmans|author3=S. Javed|author4=P. Narayanamurthy|title=Robust PCA and Robust Subspace Tracking|journal=Preprint|volume= 35|issue= 4|pages= 32–55|arxiv= 1711.09492| year=2017|bibcode=2017arXiv171109492V|doi= 10.1109/MSP.2018.2826566}}
16. ^{{Cite journal|last=T. Bouwmans|author2= A. Sobral|author3= S. Javed|author4= S. Jung|author5= E. Zahzahg|title=Decomposition into Low-rank plus Additive Matrices for Background/Foreground Separation: A Review for a Comparative Evaluation with a Large-Scale Dataset |journal= Computer Science Review|volume= 23|pages= 1–71|arxiv=1511.01245|year=2015|doi= 10.1016/j.cosrev.2016.11.001}}
17. ^{{cite journal|last=Z. Lin|title=A Review on Low-Rank Models in Data Analysis|journal=Big Data and Information Analytics|volume=1|issue=2|pages=139–161|year=2016|doi=10.3934/bdia.2016001}}
External links
- [https://github.com/andrewssobral/lrslibrary#lrslibrary LRSLibrary]
- Mandagapattu Tirumurti Temple
- Mandagarana
- Mandagere Subbarao Krishnamurthy
- Mandag Morgen
- Mandagomphodon
- Mandagomphodon hirschoni
- Mandagomphodon hirschsoni
- Mandagsbarn
- Manda Hararo
- Mandahl
- Mandahuaca language
- Mandaic Aramaic
- Mandaic (disambiguation)
- Mandai Columbarium
- Mandai Crematorium
- Mandai Crematorium and Columbarium
- Mandaic (script)
- Mandaic (Unicode block)
- Mandai Depot
- Mandailing
- Mandai massacre
- Manda-Inakir Mountain
- Mandaithivu sea massacre
- Manda,Jammu
- Manda, Jammu