“Tarski's theorem about choice”的意思、由来-开放百科全书

词条

Tarski's theorem about choice

释义

Proof
References

In mathematics, Tarski's theorem, proved by {{harvs|txt|first=Alfred|last= Tarski|authorlink=Alfred Tarski|year=1924}}, states that in ZF the theorem "For every infinite set , there is a bijective map between the sets and 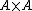" implies the axiom of choice. The opposite direction was already known, thus the theorem and axiom of choice are equivalent.

Tarski told {{harvs|first=Jan|last=Mycielski|authorlink=Jan Mycielski|year=2006|txt}} that when he tried to publish the theorem in Comptes Rendus de l'Académie des Sciences Paris, Fréchet and Lebesgue refused to present it. Fréchet wrote that an implication between two well known propositions is not a new result. Lebesgue wrote that an implication between two false propositions is of no interest.

Proof

Our goal is to prove that the axiom of choice is implied by the statement "For every infinite set : ".

It is known that the well-ordering theorem is equivalent to the axiom of choice, thus it is enough to show that the statement implies that for every set there exist a well-order.

For finite sets it is trivial, thus we will assume that is infinite.

Since the collection of all ordinals such that there exist a surjective function from to the ordinal is a set, there exist a minimal non-zero ordinal, 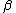, such that there is no surjective function from to .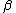

We assume without loss of generality that the sets and 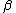are disjoint.

By our initial assumption, , thus there exists a bijection .

For every , it is impossible that , because otherwise we could define a surjective function from to .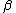

Therefore, there exists at least one ordinal 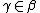, such that 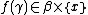, thus the set 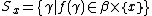is not empty.

With this fact in our mind we can define a new function: .

This function is well defined since 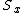is a non-empty set of ordinals, hence it has a minimum.

Recall that for every 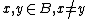the sets 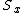and 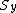are disjoint.

Therefore, we can define a well order on , for every 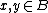we shall define 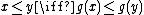, since the image of , i.e. 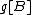, is a set of ordinals and therefore well ordered.

References

{{citation|first=Herman |last=Rubin|first2= Jean E.|last2= Rubin|author2-link= Jean E. Rubin |title= Equivalents of the Axiom of Choice II|publisher= North Holland/Elsevier|year= 1985|isbn=0-444-87708-8}}
{{citation|title=A system of axioms of set theory for the rationalists|journal=Notices of the American Mathematical Society|volume=53|issue=2|pages=209|year=2006|first=Jan|last=Mycielski|authorlink=Jan Mycielski|url=http://www.ams.org/notices/200602/fea-mycielski.pdf}}
{{citation|last=Tarski|first= A.|title= Sur quelques theorems qui equivalent a l'axiome du choix|journal=Fundamenta Mathematicae |volume= 5 |year=1924|pages= 147-154 |url=http://pldml.icm.edu.pl/pldml/element/bwmeta1.element.bwnjournal-article-fmv5i1p18bwm}}

Ordinal de Hartogs#Produit cardinal

4 : Set theory|Theorems in the foundations of mathematics|Axiom of choice|Cardinal numbers

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。