“Taut foliation”的意思、由来-开放百科全书

词条

Taut foliation

释义

Related concepts
Properties
Rummler–Sullivan theorem

In mathematics, a taut foliation is a codimension 1 foliation of a 3-manifold with the property that there is a single transverse circle intersecting every leaf. By transverse circle, is meant a closed loop that is always transverse to the tangent field of the foliation. Equivalently, by a result of Dennis Sullivan, a codimension 1 foliation is taut if there exists a Riemannian metric that makes each leaf a minimal surface.

Taut foliations were brought to prominence by the work of William Thurston and David Gabai.

Related concepts

Taut foliations are closely related to the concept of Reebless foliation. A taut foliation cannot have a Reeb component, since the component would act like a "dead-end" from which a transverse curve could never escape; consequently, the boundary torus of the Reeb component has no transverse circle puncturing it. A Reebless foliation can fail to be taut but the only leaves of the foliation with no puncturing transverse circle must be compact, and in particular, homeomorphic to a torus.

Properties

The existence of a taut foliation implies various useful properties about a closed 3-manifold. For example, a closed, orientable 3-manifold, which admits a taut foliation with no sphere leaf, must be irreducible, covered by 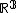, and have negatively curved fundamental group.

Rummler–Sullivan theorem

By a theorem of Rummler and Sullivan the following conditions are equivalent for transversely orientable codimension one foliations 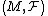of closed, orientable, smooth manifolds M:

is taut;
there is a flow transverse to which preserves some volume form on M;
there is a Riemannian metric on M for which the leaves of are least area surfaces.

2 : 3-manifolds|Foliations

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。