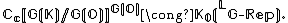“Satake isomorphism”的意思、由来-开放百科全书

词条

Satake isomorphism

释义

Statement
Notes
References

In mathematics, the Satake isomorphism, introduced by {{harvs|txt|authorlink=Ichirō Satake|last=Satake|year=1963}}, identifies the Hecke algebra of a reductive group over a local field with a ring of invariants of the Weyl group.

The geometric Satake equivalence is a geometric version of the Satake isomorphism, introduced by {{harvtxt|Mirković|Vilonen|2007}}.

Statement

Let G be a Chevalley group, K be a non-Archimedean local field and O be its ring of integers. Then the Satake isomorphism identifies the Grothendieck group of complex representations of the Langlands dual 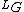of G, with the ring of G(O) invariant compactly supported functions on the affine Grassmannian. In formulas:

Here G(O) acts on G(K) / G(O) by multiplication from the left.

Notes

References

{{Citation | last1=Gross | first1=Benedict H. |authorlink=Benedict Gross| title=Galois representations in arithmetic algebraic geometry (Durham, 1996) | publisher=Cambridge University Press | series=London Math. Soc. Lecture Note Ser. | doi=10.1017/CBO9780511662010.006 | mr=1696481 | year=1998 | volume=254 | chapter=On the Satake isomorphism | pages=223–237}}
{{Citation | last1=Mirković | first1=I. | last2=Vilonen | first2=K. | title=Geometric Langlands duality and representations of algebraic groups over commutative rings | doi=10.4007/annals.2007.166.95 | mr=2342692 | year=2007 | journal=Annals of Mathematics |series=Second Series | issn=0003-486X | volume=166 | issue=1 | pages=95–143 |arxiv=math/0401222}}
{{Citation | last1=Satake | first1=Ichirō |authorlink=Ichirō Satake| title=Theory of spherical functions on reductive algebraic groups over p-adic fields | url=http://www.numdam.org/item?id=PMIHES_1963__18__5_0 | mr=0195863 | year=1963 | journal=Publications Mathématiques de l'IHÉS | issn=1618-1913 | issue=18 | pages=5–69}}

1 : Representation theory

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。