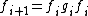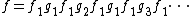“Sesquipower”的意思、由来-开放百科全书

词条

Sesquipower

释义

Formal definition
Bi-ideal sequence
Unavoidable patterns
Sesquipowers in infinite sequences
See also
References

In mathematics, a sesquipower or Zimin word is a string over an alphabet with identical prefix and suffix. Sesquipowers are unavoidable patterns, in the sense that all sufficiently long strings {{clarify span|contain|reason=Distinguish from the usual meaning ('contains as substring').|date=March 2019}} one.

Formal definition

Formally, let A be an alphabet and A^∗ be the free monoid of finite strings over A. Every non-empty word w in A⁺ is a sesquipower of order 1. If u is a sesquipower of order n then any word w = uvu is a sesquipower of order n + 1.^[1] The degree of a non-empty word w is the largest integer d such that w is a sesquipower of order d.^[2]

Bi-ideal sequence

A bi-ideal sequence is a sequence of words f_i where f₁ is in A⁺ and

for some g_i in A^∗ and i ≥ 1. The degree of a word w is thus the length of the longest bi-ideal sequence ending in w.^[2]

Unavoidable patterns

For a finite alphabet A on k letters, there is an integer M depending on k and n, such that any word of length M has a factor which is a sesquipower of order at least n. We express this by saying that the sesquipowers are unavoidable patterns.^[3]^[4]

Sesquipowers in infinite sequences

Given an infinite bi-ideal sequence, we note that each f_i is a prefix of f_i+1 and so the f_i converge to an infinite sequence

We define an infinite word to be a sesquipower if it is the limit of an infinite bi-ideal sequence.^[5] An infinite word is a sesquipower if and only if it is a recurrent word,^[5]^[8] that is, every factor occurs infinitely often.^[6]

Fix a finite alphabet A and assume a total order on the letters. For given integers p and n, every sufficiently long word in A^∗ has either a factor which is a p-power or a factor which is an n-sesquipower; in the latter case the factor has an n-factorisation into Lyndon words.^[7]

References

1. ^Lothaire (2011) p. 135
2. ^¹Lothaire (2011) p. 136
3. ^Lothaire (2011) p. 137
4. ^Berstel et al (2009) p.132
5. ^¹Lothiare (2011) p. 141
6. ^Lothaire (2011) p. 30
7. ^¹Berstel et al (2009) p.133

{{cite book | last1=Berstel | first1=Jean | last2=Lauve | first2=Aaron | last3=Reutenauer | first3=Christophe | last4=Saliola | first4=Franco V. | author1-link = Jean Berstel | title=Combinatorics on words. Christoffel words and repetitions in words | series=CRM Monograph Series | volume=27 | location=Providence, RI | publisher=American Mathematical Society | year=2009 | isbn=978-0-8218-4480-9 | url=http://www.ams.org/bookpages/crmm-27 | zbl=1161.68043 }}
{{cite book | last=Lothaire | first=M. | authorlink=M. Lothaire | title=Algebraic combinatorics on words | others=With preface by Jean Berstel and Dominique Perrin | edition=Reprint of the 2002 hardback | series=Encyclopedia of Mathematics and Its Applications | volume=90| publisher=Cambridge University Press | year=2011 | isbn=978-0-521-18071-9 | zbl=1221.68183 }}
{{cite book | last=Pytheas Fogg | first=N. | editor1=Berthé, Valérie|editor1-link=Valérie Berthé|editor2=Ferenczi, Sébastien|editor3=Mauduit, Christian|editor4=Siegel, Anne | title=Substitutions in dynamics, arithmetics and combinatorics | series=Lecture Notes in Mathematics | volume=1794 | location=Berlin | publisher=Springer-Verlag | year=2002 | isbn=3-540-44141-7 | zbl=1014.11015 }}

3 : Semigroup theory|Formal languages|Combinatorics on words

随便看

开放百科全书收录14589846条英语、德语、日语等多语种百科知识，基本涵盖了大多数领域的百科知识，是一部内容自由、开放的电子版国际百科全书。

Formal definition

Bi-ideal sequence

Unavoidable patterns

Sesquipowers in infinite sequences

See also

References